1 Introducción a la lógica

1.1 Lógica proposicional

La lógica matemática es una teoría analítica del arte de razonar y uno de sus principales objetivos es sistematizar (codificar) los principios que rigen los razonamientos válidos.

Es una teoría axiomática intuitiva, que tiene como uno de sus propósitos fundamentales el de clasificar los razonamientos dentro de dos clases: los válidos y los no válidos. De manera informal, diremos que un razonamiento es válido cuando nos permite obtener conclusiones verdaderas si se ha comenzado con proposiciones verdaderas (hipótesis). En cambio, un razonamiento que a partir de proposiciones verdaderas produzca conclusiones falsas, no es un razonamiento válido.

Conceptos primitivos. Verdad y falsedad.

Comenzaremos con los conceptos primitivos de Falso (F o 0) y de Verdadero (V o 1). Decimos que ambos conceptos son primitivos porque no los explicamos en términos de conceptos más elementales.

Definición 1.1 Diremos que una proposición es cualquier afirmación de la que pueda decidirse si es falsa o verdadera. Una afirmación (y por lo tanto una proposición) no puede ser falsa y verdadera a la vez, este es el principio del tercero excluido.

Ejemplo 1.1 Determinar si las siguientes afirmaciones son proposiciones.

Un perro es un mamífero.
México es el país con mayor número de habitantes.
Esta frase es falsa.
Hay un número mayor que todos los demás.
Si un animal pone huevos entonces es un ave o es un reptil.

1.2 Conectivos lógicos y tablas de verdad

Para formar nuevas proposiciones a partir de otras usaremos los conectivos lógicos:

\[\begin{equation*} \lnot, \qquad \wedge, \qquad \vee ,\qquad \Rightarrow, \qquad \Leftrightarrow \end{equation*}\]

De tal manera que si \(p\) y \(q\) son proposiciones entonces también lo son:

\[\begin{equation*} \lnot p, \qquad p\wedge q, \qquad p\vee q,\qquad p\Rightarrow q, \qquad p\Leftrightarrow q, \end{equation*}\]

denotaremos la equivalencia lógica de dos proposiciones como \(p\equiv q\).

La calidad de falsa o verdadera que tiene una proposición como las anteriores, depende de la calidad de falso o verdadero que tengan las proposiciones que la componen. Definiremos los conectivos lógicos mediante tablas de verdad.

1.2.1 Negación

Si \(p\) es una proposición, denotaremos su negación por \(\lnot p\), la cual se lee no p.

Definición 1.2 El conectivo \(\lnot\) queda definido por medio de la tabla:

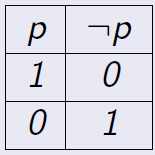
Entonces \(\lnot p\) es una proposición verdadera cuando \(p\) es falsa, o bien, es falsa cuando \(p\) es verdadera.

1.2.2 Conjunción.

Si \(p\), \(q\) son proposiciones su conjunción

\[\begin{equation*} p\wedge q \end{equation*}\]

(léase: \(p\) y \(q\)) es la proposición que es verdadera cuando tanto \(p\) como \(q\) son verdaderas.

Definición 1.3 El conectivo lógico conjunción, \(\wedge\) se define mediante la siguiente tabla,

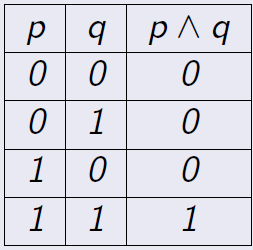
Luego, \(p\wedge q\) es falsa si alguna de las proposiciones (o ambas) es falsa.

1.2.3 Disyunción

Cuando \(p\) y \(q\) son proposiciones, podemos formar su disyunción \(p\vee q\), que se lee: \(p\) o \(q\).

\(p\vee q\) es falsa sólo cuando tanto \(p\) como \(q\) son falsas. Así, basta con que una de las proposiciones sea verdadera para que su disyunción sea verdadera.

Definición 1.4 El conectivo lógico disyunción, \(\vee\), se define mediante la siguiente tabla,

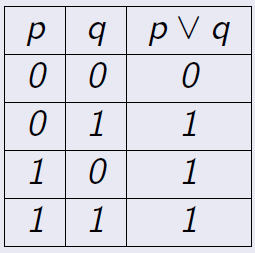
\(p\vee q\) es falsa cuando tanto \(p\) como \(q\) lo son.

1.2.4 El conectivo implicación.

Dadas la proposiciones \(p\), \(q\), definimos la proposición \(p\Rightarrow q\) (\(p\) implica \(q\)) como la proposición que es cierta cuando \(p\) es falsa o \(q\) es verdadera. Así, si se tiene que tanto \(p \Rightarrow q\) como \(p\) son verdaderas, sería porque \(q\) es verdadera.

Definición 1.5 El conectivo lógico implicación, \(\Rightarrow\), se define por medio de la siguiente tabla,

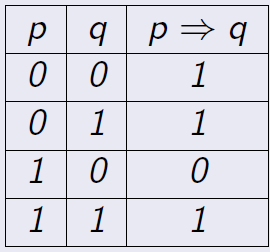
\(p\Rightarrow q\), se lee \(p\) implica \(q\), si \(p\) entonces \(q\), \(p\) sólo si \(q\), \(p\) es condición suficiente para \(q\), \(q\) es condición necesaria para \(p\).

\(p\Rightarrow q\) es falsa cuando \(p\) es verdadera y \(q\) es falsa.

1.2.5 Conectivo doble implicación.

Definición 1.6 El conectivo lógico doble implicación, \(\Leftrightarrow\), tiene la misma tabla de verdad que \((p\Rightarrow q)\wedge (q\Rightarrow p)\).

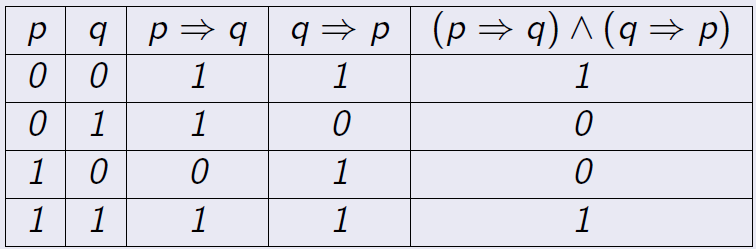
Es decir

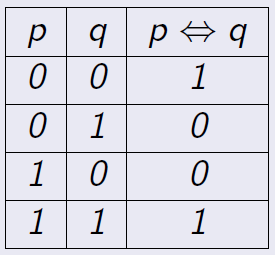
Así que \(p \Leftrightarrow q\) es verdadera cuando los valores de verdad de \(p\) y de \(q\) coinciden. \(p \Leftrightarrow q\) se lee \(p\) si y sólo si \(q\), \(p\) es equivalente a \(q\), \(p\) es condición necesaria y suficiente para \(q\).

1.3 Tautologías y absurdos.

Ejemplo 1.2 Verifíquese la tabla de verdad de: \(p\wedge(q\vee r) \Leftrightarrow (p\wedge q) \vee (p\wedge r)\)

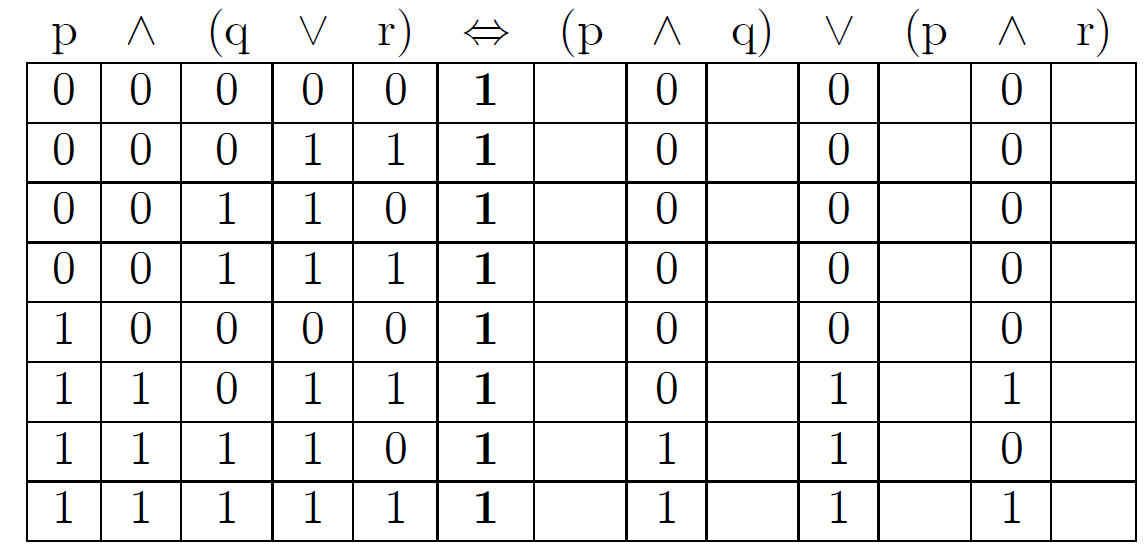
Ejemplo 1.3 Realizar la tabla de verdad de \(\lnot (p\wedge q)\Leftrightarrow (\lnot p) \vee (\lnot q)\)

Notemos que en las proposiciones anteriores siempre tienen el valor de verdad 1. Las proposiciones con esta propiedad, que son verdaderas independientemente de los valores de verdad de sus proposiciones componentes, se llaman tautologías.

En el otro extremo, las proposiciones que son falsas independientemente de los valores de verdad de sus proposiciones componentes, se llaman contradicciones o absurdos, las cuales serán denotadas por \(\nabla\).

Algunas tautologías importantes.

\(p\wedge(q\vee r) \Leftrightarrow (p\wedge q) \vee (p\wedge r)\) (distributividad de \(\wedge\) sobre \(\vee\)).
\(p\vee(q\wedge r) \Leftrightarrow (p\vee q) \wedge (p\vee r)\) (distributividad de \(\vee\) sobre \(\wedge\)).
\(p \wedge (q\wedge r) \Leftrightarrow (p\wedge q) \wedge r\) (asociatividad para \(\wedge\)).
\(p \vee (q\vee r) \Leftrightarrow (p\vee q) \vee r\) (asociatividad para \(\vee\)).
\(\lnot (p\vee q)\Leftrightarrow (\lnot p \wedge \lnot q)\) (ley de De Morgan).
\(\lnot (p\wedge q)\Leftrightarrow (\lnot p \vee \lnot q)\) (ley de De Morgan).
\((p\vee q)\Leftrightarrow (q\vee p)\) (conmutatividad para \(\vee\)).
\((p\wedge q)\Leftrightarrow (q\wedge p)\) (conmutatividad para \(\wedge\)).
\(\lnot (p\Rightarrow q)\Leftrightarrow (p\wedge \lnot q)\)
\((p\Rightarrow q) \Leftrightarrow (\lnot q \Rightarrow \lnot p)\) (contrapositiva).
\((p\Leftrightarrow q) \Leftrightarrow (\lnot p\Leftrightarrow \lnot q)\).
\(\lnot (\lnot p) \Leftrightarrow p\) (doble negación)

Ejemplo 1.4 Verificar que la implicación, \(\Rightarrow\), no es asociativa.

Ejemplo 1.5 \(p\Rightarrow (q\Rightarrow p)\) es una tautología

Ejemplo 1.6 Demostrar que \((p\wedge q)\Rightarrow p\) (Simplificación) es una tautología.

Ejemplo 1.7 Demostrar que \(p\Rightarrow (p\vee q)\) (Adición) es una tautología.

1.4 Predicados

Las constantes extralógicas son símbolos que se utilizan para referirse a elementos específicos en el universo de trabajo o conjunto de referencia. Por otro lado, las variables, que usualmente denotamos por \(x, y,...\), con o sin subíndices, no tienen valores determinados.

Ejemplo 1.8

\(a\) es un número real tal que \(a^3=-1\).
\(a\) es un número entero tal que \(0 <a<2\).
\(p(x):\qquad x>1\).
\(q(x):\) El número \(x+2\) es un entero par.

Definición 1.7 Una frase declarativa es un predicado (o proposición abierta) si contiene una o más variables, y no es una proposición, pero se convierte en una proposición cuando las variables que aparecen en ella se reemplazan por ciertas opciones permisibles (elementos del conjunto de referencia).

Ejemplo 1.9 Sean \(p(x)\), \(q(x)\) los siguientes predicados:

\[\begin{equation*} p(x): \, x\leq 3, \qquad \, q(x):\, x+1 \text{ es impar}. \end{equation*}\]

Si el conjunto de referencia consta de todos los enteros. ¿cuáles son los valores de verdad de las siguientes proposiciones?

\[\begin{align*} a)&p(1) & b)&q(1) & c)&\neg p(3) \\ d)&q(6) & e)&p(7)\vee q(7) & f)&p(3) \wedge q(4)\\ g)&p(4) & h)&\neg (p(-4)\vee q(-3)) & i)& \neg p(-4)\wedge \neg q(-3) \end{align*}\]

1.5 Cuantificadores

Consideremos un predicado \(p(x)\) donde \(x\) toma valores en un conjunto de referencia \(X\) y que para cada valor específico de \(x\), \(p(x)\) es verdadera; esto puede ser expresado de la forma

\[\begin{equation*} \text{para todo } x \, p(x)\quad \text{ o bien }\quad \forall x \, p(x). \end{equation*}\]

A \(\forall\) se le llama el cuantificador universal. Ahora, si \(p(x)\) es verdadera para el menos un valor de \(x\) (no necesariamente todos los valores de \(X\)) decimos

\[\begin{equation*} \text{existe } x \text{ tal que }\, p(x)\quad \text{ o bien } \quad \exists x: p(x). \end{equation*}\]

A \(\exists\) se le denomina el cuantificador existencial.

1.6 Algunos métodos de demostración

1.6.1 Definiciones preliminares

Definición 1.8 Un número entero \(x\) es par si existe un entero \(z\) tal que \(x=2z\) y un número entero es impar si no es par. De manera específica, un número entero \(x\) es impar si existe un entero \(w\) tal que \(x= 2w+1\), o bien, un entero \(w'\) tal que \(x=2w'-1\).

Definición 1.9 Dados dos enteros \(m\) y \(n\), diremos que \(m\) divide a \(n\), o que \(n\) es divisible por \(m\) si existe un entero \(r\) tal que \(m\cdot r=n\)

Notación. Si \(m\) divide a \(n\) lo denotamos por \(m|n\) y si \(m\) no divide a \(m\) lo denotamos \(m\nmid n\).

Definición 1.10 Un entero \(p>1\) se llama primo si su único divisor mayor que 1 es \(p\). A los enteros que no son primos los llamaremos compuestos.

1.6.2 Demostración directa

Para demostrar \(P\Rightarrow Q\), tenemos que cuando \(P\) y \(P\Rightarrow Q\) son verdaderas necesariamente \(Q\) es verdadera (modus ponens).

Ejemplo 1.10 Dar una demostración directa de las siguientes proposiciones.

Para todos los enteros \(m\) y \(n\), si \(m\) y \(n\) son pares, entonces \(m+n\) es par.
Para todos los enteros \(m\) y \(n\), si \(m+n\) es par, entonces \(m\) y \(n\) son los dos pares o los dos impares.

1.6.3 Demostración por contraposición

Una proposición del tipo \(P\Rightarrow Q\) es tautológicamente equivalente a \((\lnot Q)\Rightarrow (\lnot P)\).

Ejemplo 1.11 Dar una demostración por contraposición de las siguientes proposiciones.

Para todo entero \(m\), si \(m\) es par, entonces \(m+7\) es impar.

Para todos los enteros \(m\) y \(n\) si \(mn>25\), entonces \(m>5\) o \(n>5\).

1.6.4 Demostración por reducción al absurdo

Si se quiere demostrar que \(P\Rightarrow Q\) es verdadera, suponer que \(P\) y \(\lnot Q\) verdaderas nos llevará a una contradicción del tipo \(R\wedge (\lnot R)\).

Ejemplo 1.12 Dar una demostración por reducción al absurdo de la siguiente afirmación: si se distribuyen 40 monedas en nueve bolsas de manera que cada bolsa contenga al menos una moneda, al menos dos bolsas contienen el mismo número de monedas.

Ejemplo 1.13 Sea

\[\begin{equation*} A=\frac{a_1+a_2+\cdots +a_n}{n} \end{equation*}\]

el promedio de los números reales \(a_1, a_2, ..., a_n\). Demuestre por reducción al absurdo que existe \(i\) tal que \(a_i\geq A\).

1.6.5 Demostración por casos

La proposición \((P_1\vee P_2)\Rightarrow Q\), es tautológicamente equivalente a \((P_1\Rightarrow Q)\wedge (P_2\Rightarrow Q)\).