8 Los números complejos
El sistema de los números complejos, denotado por \(\mathbb{C}\), está definido por
\[\begin{equation} \mathbb{C}=\{a+bi| a,b\in \mathbb{R}, i^2=-1\} \end{equation}\]
Además, \(a+bi=c+di\) si y sólo si \(a=c\) y \(b=d\).
Definición 8.1 En el conjunto de los números complejos se define la adición de la siguiente manera:
\[\begin{equation} (a+bi)+(c+di)=(a+c)+(b+d)i, \end{equation}\]
y la multiplicación está dada por:
\[\begin{equation} (a+bi)\cdot (c+di)=(ac-bd)+(ad+bc)i. \end{equation}\]
La multiplicación se puede llevar a cabo con las propiedades distributivas usuales recordando que \(i^2=-1\).
Definición 8.2 Dado un número complejo \(z=a+bi\), decimos que su parte real es \(Re(z)=a\) y su parte imaginaria es \(Im(z)=b\).
Nótese que si \(z=a+bi\) es tal que \(Im(b)=0\), entonces, \(z\in \mathbb{R}\).
Teorema 8.1 Los números complejos \(\mathbb{C}\) con las operaciones de adición y multiplicación definidas previamente forman un campo.
Es decir, satisfacen:
Axioma C1. Leyes conmutativas. Para cualesquiera \(z, w\in \mathbb{C}\)
\[\begin{eqnarray} z+w &=& w+z\\ z\cdot w& =& w\cdot z \end{eqnarray}\]
Axioma C2. Leyes asociativas. Para cualesqueira \(z, w, s \in \mathbb{C}\)
\[\begin{eqnarray} z+(w+s) &=& (z+w)+s\\ z\cdot (w\cdot s) &=& (z\cdot w)\cdot s \end{eqnarray}\]
Axioma C3. Leyes distributivas. Para cualesqueira \(z, w, s \in \mathbb{C}\)
\[\begin{eqnarray} z\cdot (w+s) &=& z\cdot w+ z\cdot s\\ (z+w)\cdot s &=& z\cdot s+ w\cdot s \end{eqnarray}\]
Axioma C4. Elementos identidad. \(\exists \,0,1\in \mathbb{C}, \, 0\neq 1\), tales que \(\forall z \in \mathbb{C}\)
\[\begin{eqnarray} z + 0 &=& z = 0+z\\ z\cdot 1 &=& z = 1\cdot z \end{eqnarray}\]
Axioma C5. Elementos inversos. Para cualesquiera \(z, w\in \mathbb{C}\), con \(w\neq 0\) \(\exists \,x,y \in \mathbb{C}\) tales que
\[\begin{eqnarray} z+x &=& 0 = x+z\\ w\cdot y& =& 1 = y\cdot w \end{eqnarray}\]
\(x\) y \(y\) se denotan por \(-z\) y \(w^{-1}\), respectivamente.
El elemento \(0\) del axioma \(C4\) se denomina el elemento identidad para la adición o cero. El elemento \(1\) es el elemento identidad para la multiplicación o uno. Estos elementos identidad son los únicos que satisfacen las propiedades que les confiere el axioma \(C4\).
El número complejo \(—z\) del axioma \(C5\) se llama el inverso aditivo de \(z\) o negativo de \(z\), mientras que el inverso multiplicativo \(w^{-1}\) de un número complejo \(w\), distinto de cero, se llama el recíproco (o inverso multiplicativo) de \(w\).
Dado un número complejo \(z=a+bi\) diferente de cero tenemos:
\[\begin{equation} z^{-1}=\frac{1}{a+bi}=\frac{a-bi}{(a+bi)(a-bi)}=\frac{a-ib}{a^2+b^2}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i \end{equation}\]
Para obtener el inverso multiplicativo de \(z\), se multiplicó por \(1=(a-ib)/(a-ib)\). Posteriormente se brindará una definición para este número complejo.
A diferencia del conjunto de los números reales, el campo de los números complejos no tiene un orden.
Cada número complejo \(z=a+bi\) es asociado con un elemento \((a,b)\) en \(\mathbb{R}^2\) y podemos interpretarlo como un punto en el plano complejo, donde eje horizontal es denominado el eje real y el vertical el eje imaginario.
Definición 8.3 Dado un número complejo \(z=a+bi\), su valor absoluto o módulo es el número real \(|z|=\sqrt{a^2+b^2}\). El punto del plano correspondiente al complejo \(z\) es \((a,b)\) y \(|z|\) es la distancia del origen \((0,0)\) al punto \((a,b)\).
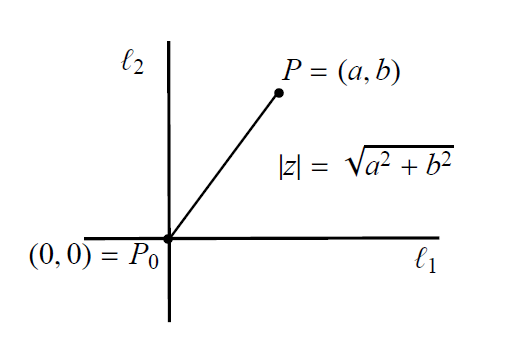
Definición 8.4 Dado un número complejo \(z=a+bi\), su conjugado denotado por \(\overline{z}\), es \(\overline{z}=a-bi\).
Observación. El módulo de \(z\in \mathbb{C}\) se puede calcular como \(|z|=\sqrt{z\overline{z}}\).
A continuación se enuncián algunas propiedades de la conjugación de números complejos.
Teorema 8.2 Sean \(z,w\in \mathbb{C}\). Entonces
\(\overline{z}=z\) si y sólo si \(Im(z)=0\), es decir, \(z\in \mathbb{R}\).
\(\overline{z}=-z\) si y sólo si \(Re(z)=0\).
\(\overline{(-z)}=-\overline{z}\).
\(\overline{\overline{z}}=z\).
\(\overline{(z+w)}=\overline{z}+\overline{w}\).
\(\overline{(z-w)}=\overline{z}+\overline{w}\).
\(\overline{(z\cdot w)}=\overline{z}\cdot\overline{w}\).
Si \(w\neq0\) entonces \(\overline{w}\neq 0\) y \(\overline{\left(\frac{z}{w}\right)}=\left(\frac{\overline{z}}{\overline{w}}\right)\). En particular \(\overline{(w^{-1})}=(\overline{w})^{-1}\).
\(z+\overline{z}=2Re(z)\) y \(z-\overline{z}=2Im(z)i\).
Si \(z=a+bi\), entonces \(z\cdot \bar{z}=a^2+b^2\), es decir que \(z\cdot \bar{z}\in \mathbb{R}^+\cup\{0\}\).