1 Preliminares Matemáticas
Aquí se incluirán, las definiciones y teoremas necesarios para desarrollar algunos de los métodos numéricos.
1.1 Límites y continuidad
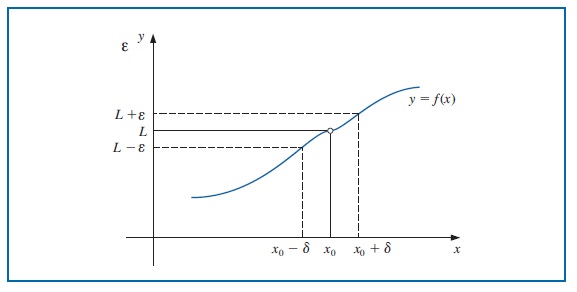
Definición 1.1 Una función \(f:X\subset \mathbb{R}\rightarrow \mathbb{R}\) tiene el límite \(L\) cuando \(x\) tiende a \(x_0\), denotado por
\[\begin{equation} \lim_{x \rightarrow x_0} f (x) = L, \end{equation}\]
si, dado cualquier número real \(\varepsilon > 0\), existe un número real \(\delta > 0\), de tal forma que \(| f (x) − L| < \varepsilon\), siempre que \(x \in X\) y \(0 < |x − x_0| < \delta\).
Definición 1.2 Sea \(f:X\subset \mathbb{R}\rightarrow \mathbb{R}\) una función y \(x_0 \in X\). Entonces \(f\) es continua en \(x_0\) si
\[\begin{equation} \lim_{x\rightarrow x_0} f(x)=f(x_0) \end{equation}\]
La función \(f\) es continua en el conjunto \(X\) si es continua en cada \(x\in X\).
El conjunto de todas las funciones que son continuas en el conjunto \(X\) se denota como \(C(X)\).
Definición 1.3 Sea \(\{x_n\}_{n=1}^\infty\) una sucesión infinita de números reales. Esta sucesión tiene el límite \(x\) (converge a \(x\)) si, para cualquier \(\varepsilon >0\) , existe un entero positivo \(N(\varepsilon)\) tal que \(|x_n−x| < \varepsilon\) siempre que \(n > N(\varepsilon)\). La notación
\[\begin{equation} \lim_{n\rightarrow \infty} x_n=x \quad \text{ o } \quad x_n\rightarrow x \end{equation}\]
significa que la sucesión \(\{x_n\}_{n=1}^\infty\) converge a \(x\).
Teorema 1.1 Si \(f: X\subset \mathbb{R}\rightarrow \mathbb{R}\) y \(x_0\in X\), entonces los siguientes enunciados son equivalentes:
\(f\) es continua en \(x_0\);
Si \(\{x_n\}_{n=1}^\infty\) es cualquier sucesión en \(X\), que converge a \(x_0\), entonces \(\lim_{n\rightarrow \infty} f (x_n) = f (x_0)\).
Se supondrá que las funciones que consideraremos al analizar los métodos numéricos son continuas.
1.2 Diferenciabilidad
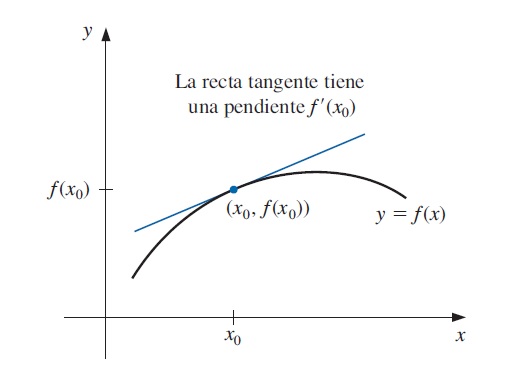
Definición 1.4 Si \(f\) es una función definida en un intervalo abierto que contiene a \(x_0\). La función \(f\) es diferenciable en \(x_0\) si
\[\begin{equation} f'(x_0)=\lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0} \end{equation}\]
existe. El número \(f'(x_0)\) recibe el nombre de derivada de \(f\) en \(x_0\). Una función que tiene una derivada en cada número en un conjunto \(X\) es diferenciable en \(X\).
La derivada de \(f\) en \(x_0\) es la pendiente de la recta tangente a la gráfica de \(f\) en \((x_0, f(x_0))\).
Teorema 1.2 Si una función \(f\) es diferenciable en \(x_0\), entonces \(f\) es continua en \(x_0\).
El conjunto de todas las funciones que tienen \(n\) derivadas continuas en \(X\) se denota como \(C^n(X)\) y el conjunto de funciones que tienen derivadas de todos los órdenes en \(X\) se denota como \(C^\infty(X)\).
Teorema 1.3 Rolle. Suponga que \(f \in C[a, b]\) y \(f\) es diferenciable en \((a, b)\). Si \(f(a) = f (b)\), entonces existe un número \(c\in (a,b)\) con \(f'(c)=0\).

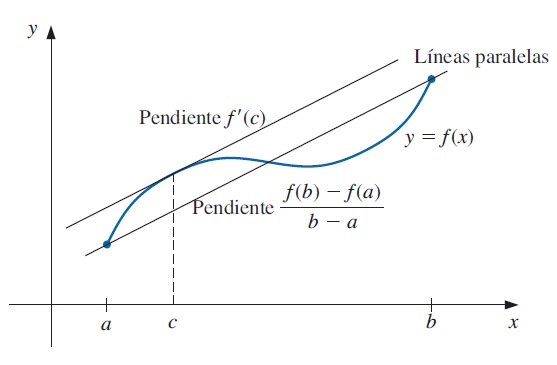
Teorema 1.4 Valor medio. Si \(f\in C[a,b]\) y \(f\) es diferenciable en \((a,b)\), entonces existe un número \(c\in (a,b)\) tal que
\[\begin{equation} f'(c)=\frac{f(b)-f(a)}{b-a}. \end{equation}\]
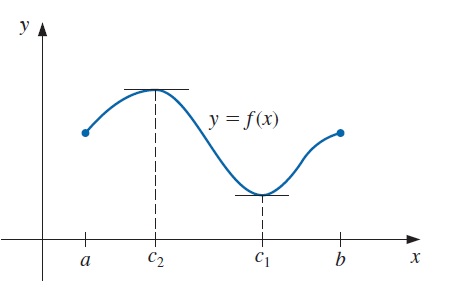
Teorema 1.5 Valor extremo. Si \(f\in C[a,b]\) entonces existen \(c_1, c_2\in [a,b]\) con \(f(c_1)\leq f(x)\leq f(c_2)\), para todas las \(x\in [a,b]\). Además, si \(f\) es diferenciable en \((a,b)\), entonces se presentan los números \(c_1\) y \(c_2\) ya sea en los extremos de \([a,b]\) o donde \(f'\) es cero.
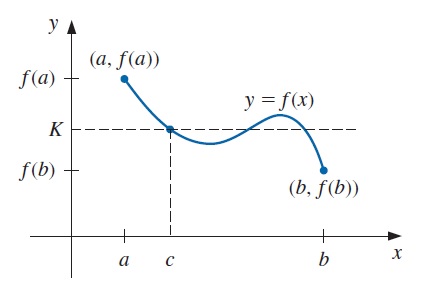
Teorema 1.6 Valor intermedio. Si \(f\in C[a, b]\) y \(K\) es cualquier número entre \(f(a)\) y \(f(b)\), entonces existe un número \(c\in (a,b)\) para el cual \(f(c)= K\).
1.3 Integración.
Definición 1.5 La integral de Riemann de la función \(f\) en el intervalo \([a, b]\) es el siguiente límite, siempre y cuando exista:
\[\begin{equation} \int_a^b f(x)\,dx=\lim_{\Delta x_i\rightarrow 0}\sum_{i=1}^nf(z_i)\Delta x_i, \end{equation}\]
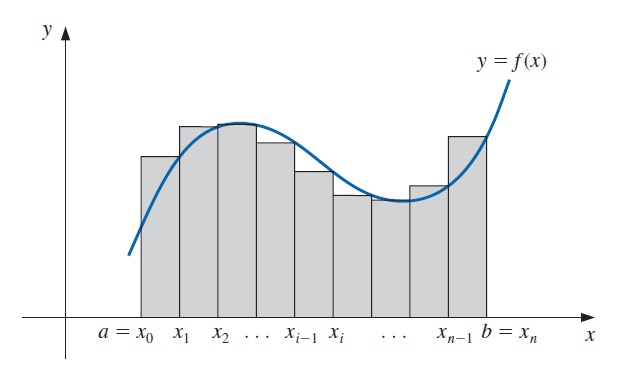
donde los números \(x_0, x_1,\dots , x_n\) satisfacen \(a = x_0 \leq x_1 \leq \dots \leq x_n= b\), donde \(\Delta x_i = x_i − x_{i−1}\), para cada \(i = 1, 2,\cdots ,n\), y \(z_i\) se selecciona de manera arbitraria en el intervalo \([ x_{i−1}, x_i]\).
Una función \(f\) que es continua en un intervalo \([a, b]\) es también Riemann integrable en \([a, b]\). Esto nos permite elegir, para conveniencia computacional, los puntos \(x_i\) se separarán uniformemente en \([a, b]\) para cada \(i = 1, 2, \cdots , n\), para seleccionar \(z_i = x_i\). En este caso,
\[\begin{equation} \int_a^bf(x)\,dx=\lim_{n\rightarrow \infty} \frac{b-a}{n}\sum_{i=1}^n f(x_i) \end{equation}\]
donde los números mostrados en la siguiente figura, como \(x_i\), son \(x_i=a+i(b-a)/n\).
Teorema 1.7 Valor promedio para integrales. Suponga que \(f\in C[a,b]\), la integral de Riemann de \(g\) existe en \([a,b]\), y \(g(x)\) no cambia de signo en \([a,b]\). Entonces existe un número \(c\in (a,b)\) con
\[\begin{equation} \int_a^b f(x)g(x)dx=f(c)\int_a^b g(x)dx. \end{equation}\]
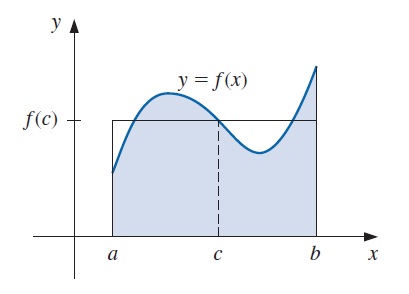
Cuando \(g(x)=1\), el teorema anterior es el teorema del valor medio para integrales. Éste proporciona el valor promedio de la función \(f\) sobre el intervalo \([a, b]\) como
\[\begin{equation} f(c)=\frac{1}{b-a}\int_a^b f(x)\,dx \end{equation}\]
1.4 Polinomios y series de Taylor.
Teorema 1.8 Taylor. Suponga que \(f\in C^n[a,b]\), \(f^{(n+1)}\) existe en \([a,b]\) y \(x_0\in [a,b]\). Para cada \(x\in [a,b]\), existe un número \(\xi (x)\) entre \(x_0\) y \(x\) con
\[\begin{equation} f(x)=P_n(x)+R_n(x) \end{equation}\]
donde
\[\begin{equation} \begin{aligned} P_{n}(x) &=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n} \\ &=\sum_{k=0}^{n} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k} \end{aligned} \end{equation}\]
y
\[\begin{equation} R_n(x)=\frac{f^{(n+1)}(\xi (x))}{(n+1)!}(x-x_0)^{n+1} \end{equation}\]
Aquí \(P_n(x)\) es llamado el \(n\)-ésimo polinomio de Taylor para \(f\) alrededor de \(x_0\) y \(R_n(x)\) recibe el nombre de residuo (o error de truncamiento) relacionado con \(P_n(x)\).