8 Diferenciación e integración numérica
8.1 Diferenciación numérica
La derivada de una función \(f:[a,b]\rightarrow \mathbb{R}\) en \(x_0\in (a,b)\) es
\[\begin{equation} f'(x_0)=\lim_{h\rightarrow 0}\frac{f(x_0+h)-f(x_0)}{h} \end{equation}\]
Esta ecuación nos proporciona una manera de generar una aproximación de \(f'(x_0)\);
\[\begin{equation} \frac{f(x_0+h)-f(x_0)}{h} \end{equation}\]
para valores pequeños de \(h\).
Para aproximar \(f'(x_0)\), supongamos primero que \(x_0\in (a,b)\), donde \(f\in C^2[a,b]\) y que \(x_1=x_0+h\) para alguna \(h\neq 0\), que es suficientemente pequeña para garantizar que \(x_1\in [a,b]\). Se construye el primer polinomio de Lagrange \(P_{0,1}(x)\) para \(f\) determinado por \(x_0\) y \(x_1\), con su término de error:
\[\begin{equation} \begin{aligned} f(x) &=P_{0,1}(x)+\frac{\left(x-x_{0}\right)\left(x-x_{1}\right)}{2 !} f^{\prime \prime}(\xi(x)) \\ &=\frac{f\left(x_{0}\right)\left(x-x_{0}-h\right)}{-h}+\frac{f\left(x_{0}+h\right)\left(x-x_{0}\right)}{h}+\frac{\left(x-x_{0}\right)\left(x-x_{0}-h\right)}{2} f^{\prime \prime}(\xi(x)), \end{aligned} \end{equation}\]
para algunos \(\xi(x)\) entre \(x_0\) y \(x_1\). Derivando obtenemos
\[\begin{equation} \begin{aligned} f^{\prime}(x)=& \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}+D_{x}\left[\frac{\left(x-x_{0}\right)\left(x-x_{0}-h\right)}{2} f^{\prime \prime}(\xi(x))\right] \\ =& \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}+\frac{2\left(x-x_{0}\right)-h}{2} f^{\prime \prime}(\xi(x)) \\ &+\frac{\left(x-x_{0}\right)\left(x-x_{0}-h\right)}{2} D_{x}\left(f^{\prime \prime}(\xi(x))\right) \end{aligned} \end{equation}\]
Borrando los términos relacionados con \(\xi(x)\) obtenemos
\[\begin{equation} f^{\prime}(x) \approx \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} \end{equation}\]
Cuando \(x\) es \(x_0\), sin embargo, el coeficiente de \(D_xf''(\xi(x))\) es 0 y la fórmula se simplifica en
\[\begin{equation} f^{\prime}(x_0) = \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}-\frac{h}{2}f''(\xi). \end{equation}\]
Para los valores pequeños de \(h\), el cociente de diferencia \([f(x_0+h)-f(x_0)]/h\) se puede utilizar para aproximar \(f'(x_0)\) con un error acotado por \(M|h|/2\), donde \(M\) es una cota de \(|f''(x)|\) para \(x\) entre \(x_0\) y \(x_0+h\). A esta fórmula se le conoce como fórmula de diferencias hacia adelante si \(h>0\) y como fórmula de diferencias hacia atrás si \(h<0\).
Para obtener las fórmulas generales de aproximación a la derivada, supongamos que \(\{x_0, x_1, \dots, x_n\}\) son \(n+1\) números distintos en algún intervalo \(I\) y que \(f\in C^{n+1}(I)\). Por la aproximación de \(f\) por medio de los polinomios interpolantes de Lagrange, tenemos,
\[\begin{equation} f(x)=\sum_{k=0}^n f(x_k)L_k(x)+\frac{(x-x_0)\cdots (x-x_n)}{(n+1)!} f^{(n+1)}(\xi(x)), \end{equation}\]
para algún \(\xi(x)\in I\), donde \(L_k(x)\) denota el \(k\)-ésimo coeficiente de Lagrange para \(f\) en \(x_0, x_1, \dots, x_n\). Al derivar esta ecuación obtenemos
\[\begin{equation} \begin{aligned} f'(x) &= \sum_{k=0}^n f(x_k) L_k'(x)+D_x\left[\frac{(x-x_0)\cdots (x-x_n)}{(n+1)!} \right] f^{(n+1)}(\xi (x)) \\ &+\frac{(x-x_0)\cdots (x-x_n)}{(n+1)!}D_x[f^{(n+1)}(\xi (x))] \end{aligned} \end{equation}\]
Cuando se evalúa la derivada en uno de los \(x_j\) el término que múltiplica a \(D_x[f^{(n+1)}(\xi (x))]\) es 0 y la fórmula se vuelve
\[\begin{equation} f'(x_j) = \sum_{k=0}^n f(x_k) L_k'(x_j)+\frac{f^{(n+1)}(\xi(x_j))} {(n+1)!}\prod_{k=0, k\neq j}^n(x_j-x_k) \end{equation}\]
que recibe el nombre de fórmula de \((n+1)\) puntos para aproximar \(f'(x_j)\).
8.1.1 Fórmulas de tres puntos
Puesto que
\[\begin{equation} L_0(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}, \quad \text{ tenemos }\quad L'_0(x)=\frac{2x-x_1-x_2}{(x_0-x_1)(x_0-x_2)} \end{equation}\]
De igual forma
\[\begin{equation} L'_1(x)=\frac{2x-x_0-x_2}{(x_1-x_0)(x_1-x_2)}, \quad \text{ y }\quad L'_2(x)=\frac{2x-x_0-x_1}{(x_2-x_1)(x_2-x_1)}. \end{equation}\]
Por lo tanto
\[\begin{equation} \begin{aligned} f'(x_j) &= f(x_0) \left[ \frac{2x_j-x_1-x_2}{(x_0-x_1)(x_0-x_2)}\right]+f(x_1) \left[ \frac{2x_j-x_0-x_2}{(x_0-x_1)(x_0-x_2)}\right] L_k'(x)+D_x\left[\frac{(x-x_0)\cdots (x-x_n)}{(n+1)!} \right] f^{(n+1)}(\xi (x)) \\ &+\frac{(x-x_0)\cdots (x-x_n)}{(n+1)!}D_x[f^{(n+1)}(\xi (x))] \end{aligned}\quad (*) \end{equation}\]
para cada \(j=0,1,2\), donde la notación \(\xi_j\) indica que este punto depende de \(x_j\).
Se supondrá que los nodos están espaciados de manera uniforme, es decir
\[\begin{equation} x_1=x_0+h, \quad x_2=x_0+2h, \quad \text{ para alguna } h\neq 0. \end{equation}\]
Por medio de la ecuación (*) con \(x_j=x_0, x_1=x_0+h, x_2=x_0+2h\) obtenemos
\[\begin{equation} f'(x_0)=\frac{1}{h}\left[-\frac{3}{2}f(x_0)+2f(x_1)-\frac{1}{2}f(x_2) \right]+\frac{h^2}{3}f^{(3)}(\xi_0). \end{equation}\]
Al hacer lo mismo para \(x_j=x_1\), se tiene
\[\begin{equation} f'(x_1)=\frac{1}{h}\left[-\frac{1}{2}f(x_0)+\frac{1}{2}f(x_2) \right]+\frac{h^2}{6}f^{(3)}(\xi_1), \end{equation}\]
y para \(x_j=x_2\)
\[\begin{equation} f'(x_2)=\frac{1}{h}\left[\frac{1}{2}f(x_0)-2f(x_1)+\frac{3}{2}f(x_2) \right]+\frac{h^2}{3}f^{(3)}(\xi_0). \end{equation}\]
Puesto que \(x_1=x_0+h\) y \(x_2=x_0+2h\), estas fórmulas también se pueden expresar como
\[\begin{equation} \begin{aligned} f^{\prime}\left(x_{0}\right) &=\frac{1}{h}\left[-\frac{3}{2} f\left(x_{0}\right)+2 f\left(x_{0}+h\right)-\frac{1}{2} f\left(x_{0}+2 h\right)\right]+\frac{h^{2}}{3} f^{(3)}\left(\xi_{0}\right), \\ f^{\prime}\left(x_{0}+h\right) &=\frac{1}{h}\left[-\frac{1}{2} f\left(x_{0}\right)+\frac{1}{2} f\left(x_{0}+2 h\right)\right]-\frac{h^{2}}{6} f^{(3)}\left(\xi_{1}\right), \quad y \\ f^{\prime}\left(x_{0}+2 h\right) &=\frac{1}{h}\left[\frac{1}{2} f\left(x_{0}\right)-2 f\left(x_{0}+h\right)+\frac{3}{2} f\left(x_{0}+2 h\right)\right]+\frac{h^{2}}{3} f^{(3)}\left(\xi_{2}\right) \end{aligned} \end{equation}\]
Por cuestiones de conveniencia, en la segunda ecuación se sustituye \(x_0\) por \(x_0+h\), y en la tercera \(x_0\) por \(x_0+2h\). Esto nos da tres fórmulas para aproximar \(f'(x_0)\)
\[\begin{equation} \begin{aligned} f^{\prime}\left(x_{0}\right) &=\frac{1}{2h}\left[-3\, f\left(x_{0}\right)+4 f\left(x_{0}+h\right)- f\left(x_{0}+2 h\right)\right]+\frac{h^2}{3} f^{(3)}\left(\xi_{0}\right), \\ f^{\prime}\left(x_{0}\right) &=\frac{1}{2h}\left[- f\left(x_{0}-h\right)+ f\left(x_{0}+ h\right)\right]-\frac{h^2}{6} f^{(3)}\left(\xi_{1}\right), \quad y \\ f^{\prime}\left(x_{0}\right) &=\frac{1}{2h}\left[f\left(x_{0}-2h \right)-4 f\left(x_{0}-h\right)+3 f\left(x_{0}\right)\right]+\frac{h^2}{3} f^{(3)}\left(\xi_{2}\right) \end{aligned} \end{equation}\]
Obsérvese que la última de estas ecuaciones se puede obtener a partir de la primera simplemente al reemplazar \(h\) por \(-h\), de modo que en realidad sólo son dos fórmulas:
8.1.1.1 Fórmula del extremo de tres puntos
\[\begin{equation} f^{\prime}\left(x_{0}\right) =\frac{1}{2h}\left[-3\, f\left(x_{0}\right)+4 f\left(x_{0}+h\right)- f\left(x_{0}+2 h\right)\right]+\frac{h^{2}}{3} f^{(3)}\left(\xi_{0}\right) \end{equation}\]
donde \(\xi_0\in [x_0, x_0+2h]\)
8.1.1.2 Fórmula del punto medio de tres puntos.
\[\begin{equation} f^{\prime}\left(x_{0}\right) =\frac{1}{2h}\left[f\left(x_{0}+ h\right)- f\left(x_{0}-h\right) \right]-\frac{h^{2}}{6} f^{(3)}\left(\xi_{1}\right), \end{equation}\]
donde \(\xi_1\) se encuentra entre \(x_0-h\) y \(x_0+h\).
8.1.2 Fórmulas de cinco puntos
8.1.2.1 Fórmula del punto medio de cinco puntos
\[\begin{equation} f'(x_0)=\frac{1}{12h}\left[f(x_0-2h)-8f(x_0-h)+8f(x_0+h)-f(x_0-2h) \right]+\frac{h^4}{30}f^{(5)}(\xi) \end{equation}\]
donde \(\xi\in [x_0-2h, x_0+2h]\)
8.1.2.2 Fórmula del extremo de cinco puntos
\[\begin{equation} \begin{aligned} f^{\prime}\left(x_{0}\right)=& \frac{1}{12 h}\left[-25 f\left(x_{0}\right)+48 f\left(x_{0}+h\right)-36 f\left(x_{0}+2 h\right)\right.\\ &\left.+16 f\left(x_{0}+3 h\right)-3 f\left(x_{0}+4 h\right)\right]+\frac{h^{4}}{5} f^{(5)}(\xi) \end{aligned} \end{equation}\]
donde \(\xi\) se encuentra entre \(x_0\) y \(x_0+4h\).
8.1.3 Fórmula del punto medio de la segunda derivada
\[\begin{equation} f''(x_0)=\frac{1}{h^2}\left[f(x_0-h)-2f(x_0)+f(x_0+h) \right] -\frac{h^2}{12}f^{(4)}(\xi) \end{equation}\]
Donde \(\xi \in (x_0-h, x_0+h)\).
8.2 Elementos de integración numérica.
El método básico asociado con la aproximación de \[\begin{equation} \int_a^bf(x) dx \end{equation}\] recibe el nombre de cuadratura numérica.
Éste utiliza una suma \[\begin{equation} \sum_{i=0}^n a_i f(x_i) \end{equation}\]
para aproximar \(\int_a^b f(x) dx\)
El método considerado inicialmente consiste en seleccionar un conjunto de nodos distintos \(\{x_0, ..., x_n\}\) del intervalo \([a,b]\). Posteriormente se integra el polinomio interpolante de Lagrange
\[\begin{equation} P_n(x)=\sum_{i=0}^n f(x_i)L_i(x) \end{equation}\]
y su término de error de truncamiento sobre \([a,b]\) para obtener
\[\begin{equation} \begin{aligned} \int_{a}^{b} f(x) d x &=\int_{a}^{b} \sum_{i=0}^{n} f\left(x_{i}\right) L_{i}(x) d x+\int_{a}^{b} \prod_{i=0}^{n}\left(x-x_{i}\right) \frac{f^{(n+1)}(\xi(x))}{(n+1) !} d x \\ &=\sum_{i=0}^{n} a_{i} f\left(x_{i}\right)+\frac{1}{(n+1) !} \int_{a}^{b} \prod_{i=0}^{n}\left(x-x_{i}\right) f^{(n+1)}(\xi(x)) d x, \end{aligned} \end{equation}\]
donde \(\xi(x)\) se encuentra en \([a,b]\) para cada \(x\) y
\[\begin{equation} a_i=\int_a^b L_i(x)dx \qquad\text{ para cada } i=0,1,...,n. \end{equation}\]
La fórmula de cuadratura es, por lo tanto \[\begin{equation} \int_a^bf(x) dx\approx \sum_{i=0}^n a_i f(x_i) \end{equation}\]
con un error dado por
\[\begin{equation} E(f)=\frac{1}{(n+1) !} \int_{a}^{b} \prod_{i=0}^{n}\left(x-x_{i}\right) f^{(n+1)}(\xi(x)) dx. \end{equation}\]
8.2.1 Regla trapezoidal.
\[\begin{equation} \int_a^b f(x)dx=\frac{h}{2}[f(x_0)+f(x_1)]-\frac{h^3}{12}f''(\xi). \end{equation}\]
Esta ecuación recibe el nombre de regla trapezoidal porque cuando \(f\) es una función con valores positivos \(\int_a^b f(x) dx\) se aproxima mediante el área de un trapecio.
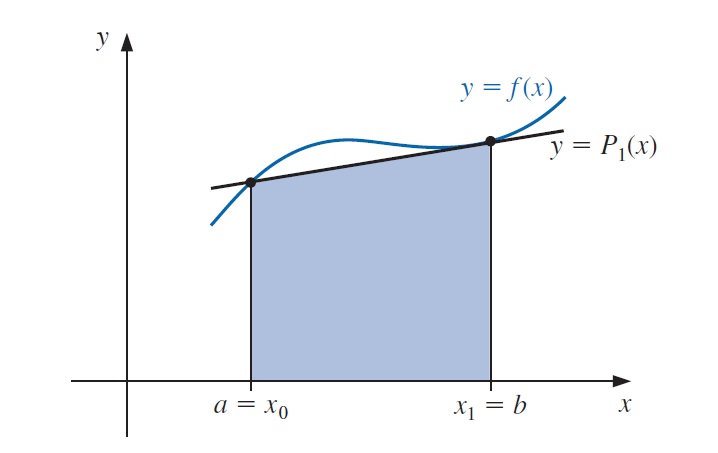
8.2.2 Regla de Simpson
La regla de Simpson resulta de la integración sobre \([a,b]\) del segundo polinomio de Lagrange con nodos igualmente espaciados \(x_0=a\), \(x_2=b\) y \(x_1=a+h\), en donde \(h=(b-a)/2\).
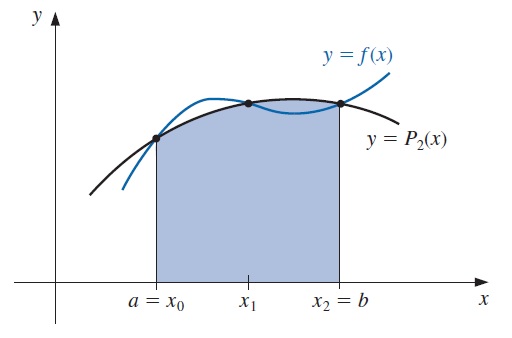
\[\begin{equation} \int_{x_0}^{x_2} f(x)\, dx=\frac{h}{3}[f(x_0)+4f(x_1)+f(x_2)]-\frac{h^5}{90}f^{(4)}(\xi) \end{equation}\]
El término de error en la regla de Simpson implica la cuarta derivada de \(f\), por lo que da resultados exactos cuando se aplica a cualquier polinomio de grado tres o menos.
8.2.3 Precisión de medición
Definición. El grado de precisión de una fórmula de cuadratura es el mayor entero positivo \(n\), de tal forma que la fórmula es exacta para \(x^k\), para cada \(k=0,1,...,n\).
Esta definición implica que las reglas trapezoidal y de Simpson tienen grados de precisión uno y tres respectivamente.
La integración y la suma son operaciones lineales; es decir,
\[\begin{equation} \int_a^b (\alpha f(x)+\beta \,g(x))\,dx=\alpha \int_a^b f(x)\,dx+\beta \int_a^b g(x)\,dx, \end{equation}\]
y
\[\begin{equation} \sum_{i=0}^n (\alpha f(x_i)+\beta \,g(x_i))=\alpha \sum_{i=0}^n f(x_i) +\beta \sum_{i=0}^n g(x_i). \end{equation}\]
para cada par de funciones integrables \(f\) y \(g\) y para cada par de constantes reales \(\alpha\) y \(\beta\). Esto implica que el grado de precisión de una fórmula de cuadratura es \(n\) si y sólo si el error es cero para todos los polinomios de grado \(k=0,1,..., n\), pero no es cero para algunos polinomios de grado \(n+1\).
Las reglas trapezoidal y de Simpson son ejemplos de una clase de métodos conocidos como fórmulas de Newton-Cotes. Existen dos tipos de fórmulas de Newton-Cotes: abiertas y cerradas.
8.2.4 Fórmulas de Newton-Cotes cerradas
La fórmula cerrada de \(n+1\) puntos de Newton Cotes utiliza nodos \(x_i=x_0+ih\), para \(i=0,1,...,n\), donde \(x_0=a\), \(x_n=b\) y \(h=(b-a)/n\). Recibe el nombre de cerrada porque los extremos del intervalo cerrado \([a,b]\) se incluyen como nodos.
\(n=1\); Regla trapezoidal
\[\begin{equation} \int_a^b f(x)\,dx=\frac{h}{2}[f(x_0)+f(x_1)]-\frac{h^3}{12}f''(\xi). \end{equation}\]
\(n=2\); Regla de Simpson
\[\begin{equation} \int_{x_0}^{x_2}f(x)\,dx=\frac{h}{3}[f(x_0)+4f(x_1)+f(x_2)]-\frac{h^5}{90}f^{(4)}(\xi) \end{equation}\]
\(n=3\); Regla de tres octavos de Simpson
\[\begin{equation} \int_{x_0}^{x_3}f(x)\,dx=\frac{3h}{8}[f(x_0)+3f(x_1)+3f(x_2)+f(x_3)]-\frac{3h^5}{80}f^{(4)}(\xi) \end{equation}\]
\(n=4\);
\[\begin{equation} \int_{x_0}^{x_4}f(x)\,dx=\frac{2h}{45}[7f(x_0)+32f(x_1)+12f(x_2)+32f(x_3)+7f(x_4)]-\frac{8h^7}{945}f^{(6)}(\xi) \end{equation}\]