9 Ecuaciones Diferenciales Ordinarias
Inicialmente se considerará aproximar la solución \(y(t)\) para un problema de la forma
\[\begin{equation} \frac{dy}{dt}=f(t,y), \quad \text{ para } a\leq t \leq b, \end{equation}\]
sujeto a la condición inicial \(y(a)=\alpha\). Posteriormente se tratará con la extensión de los métodos desarrollados hacia un sistema de ecuaciones diferenciales de primer orden de la forma
\[\begin{equation} \begin{array}{l} \frac{d y_{1}}{d t}=f_{1}\left(t, y_{1}, y_{2}, \ldots, y_{n}\right) \\ \frac{d y_{2}}{d t}=f_{2}\left(t, y_{1}, y_{2}, \ldots, y_{n}\right) \\ \quad \vdots \\ \frac{d y_{n}}{d t}=f_{n}\left(t, y_{1}, y_{2}, \ldots, y_{n}\right), \end{array} \end{equation}\]
para \(a\leq t \leq b\), sujeto a las condiciones iniciales
\[\begin{equation} y_1(a)=\alpha_1, \qquad y_2(a)=\alpha_2, ...,\qquad y_n(a)=\alpha_n. \end{equation}\]
También se examina la relación de un sistema de este tipo con el problema de valor inicial de enésimo orden de la forma
\[\begin{equation} y^{(n)}=f(t,y, y'', y'',..., y^{(n-1)}), \end{equation}\]
para \(a\leq t \leq b\), sujeto a las condiciones iniciales
\[\begin{equation} y(a)=\alpha_1, \qquad y'(a)=\alpha_2, ...,\qquad y^{(n-1)}(a)=\alpha_n. \end{equation}\]
9.1 Teoría elemental de problemas de valor inicial
Definición. Se dice que una función \(f(t,y)\) satisface la condición de Lipschitz en la variable \(y\) en un conjunto \(D\subset \mathbb{R}^2\) si existe una constante \(L>0\) con
\[\begin{equation} |f(t,y_1)-f(t,y_2)|\leq L|y_1-y_2| \end{equation}\]
siempre que \((t,y_1)\) y \((t,y_2)\) estén en \(D\). La constante \(L\) recibe el nombre de constante de Lipschitz para \(f\).
Definición. Se dice que un conjunto \(D\subset \mathbb{R}^2\) es convexo si siempre que \((t,y_1), (t,y_2)\in D\), entonces \(((1-\lambda)t_1+\lambda t_2, (1-\lambda)y_1+\lambda y_2)\) también pertenece a \(D\) para cada \(\lambda \in [0,1].\)
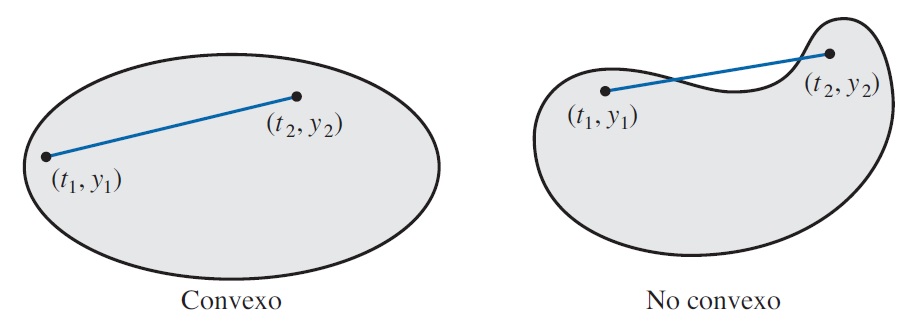
Teorema Suponga que \(f(t,y)\) se define sobre un conjunto convexo \(D\subset \mathbb{R}^2\). Si existe una constante \(L>0\) con
\[\begin{equation}\tag{1}\label{eq-1} \left|\frac{\partial f}{\partial y}(t,y)\right|\leq L, \quad \text{ para todo } (t,y)\in D, \end{equation}\]
entonces \(f\) satisface la condición de Lipschitz en \(D\) en la variable \(y\) con constante \(L\) de Lipschitz.
Teorema. Suponga que \(D=\{(t,y)| a\leq t \leq b, -\infty <y <\infty\}\) y que \(f(t,y)\) es continua en \(D\). Si \(f\) satisface la condición de Lipschitz en \(D\) para la variable \(y\), entonces el problema de valor inicial
\[\begin{equation} y'(t)=f(t,y), \qquad a\leq t \leq b, \qquad y(a)=\alpha, \end{equation}\]
tiene una única solución \(y(t)\) para \(a\leq t \leq b\).
Definición. Decimos que el problema de valor inicial
\[\begin{equation}\tag{2}\label{eq-2} \frac{dy}{dt}=f(t,y), \qquad a\leq t \leq b, \quad y(a)=\alpha \end{equation}\]
es un problema bien planteado si:
Existe una única solución, \(y(t)\).
Existen constantes \(\varepsilon_0 >0\) y \(k>0\), tales que para cualquier \(\varepsilon \in (0, \varepsilon_0)\), siempre que \(\delta(t)\) es continua con \(|\delta(t)|<\varepsilon\) para toda \(t\in [a,b]\), y cuando \(|\delta_0|<\varepsilon\), el problema de valor inicial
\[\begin{equation}\tag{3}\label{eq-3} \frac{dz}{dt}=f(t,z)+\delta (t), \qquad a\leq t \leq b, \qquad z(a)=\alpha+\delta_0 \end{equation}\]
tiene una única solución \(z(t)\) que satisface
\[\begin{equation} |z(t)-y(t)|<k\varepsilon, \qquad\forall t\in [a,b]. \end{equation}\]
El problema especificado por la ecuación \(\eqref{eq-3}\) recibe el nombre de problema perturbado relacionado con el problema original en la ecuación \(\eqref{eq-2}\). Supone la posibilidad de un error introducido en la declaración de la ecuación diferencial, así como un error \(\delta_0\) presente en la condición inicial.
El siguiente teorema especifica las condiciones que garantizan un problema de valor inicial bien planteado.
Teorema. Suponga que \(D=\{(t,y)| a\leq t \leq b, -\infty <y < \infty\}\). Si \(f\) es continua y satisface la condición de Lipschiz en la variable \(y\) sobre el conjunto \(D\), entonces el problema de valor inicial
\[\begin{equation} \frac{dy}{dt}=f(t,y), \qquad a\leq t \leq b, \quad y(a)=\alpha, \end{equation}\] está bien planteado.
9.2 Método de Euler
El objetivo del método de Euler es obtener aproximaciones para el problema de valor inicial (bien planteado)
\[\begin{equation}\tag{4}\label{eq-4} \frac{dy}{dt}=f(t,y), \qquad a\leq t\leq b,\qquad y(a)=\alpha . \end{equation}\]
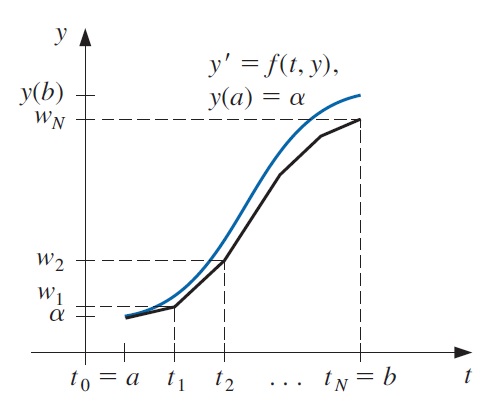
No se obtendrá una aproximación continua a la solución \(y(t)\); en su lugar, las aproximaciones para \(y\) se generarán en varios valores, llamados puntos de malla, en el intervalo \([a,b]\). Una vez que se obtiene la solución aproximada en los puntos, la solución aproximada en otros puntos en el intervalo se puede encontrar a través de interpolación.
Primero se establece que los puntos de malla están igualmente espaciados a lo largo del intervalo \([a,b]\). Esta condición se garantiza al seleccionar un entero positivo \(N\), al establecer
\[\begin{equation} h=\frac{b-a}{N}, \end{equation}\]
y seleccionar los puntos de malla
\[\begin{equation} t_i=a+ih, \qquad i=0,1,2,..., N. \end{equation}\]
La distancia común entre los puntos \(h=t_{i+1}-t_i\) recibe el nombre de tamaño de paso. Se utiliza el teorema de Taylor para deducir el método de Euler. Supongamos que \(y(t)\), la única solución para el problema de valor inicial \(\eqref{eq-4}\), tiene dos derivadas continuas en \([a,b]\), de tal forma que para cada \(i=0,1,2,..., N-1\),
\[\begin{equation} y(t_{i+1})=y(t_i)+(t_{i+1}-t_i)y'(t_i)+\frac{(t_{i+1}-t_i)^2}{2}y''(\xi_i), \end{equation}\]
para algún número \(\xi_i\in (t_i, t_{i+1})\). Puesto que \(h=t_{i+1}-t_i\), tenemos
\[\begin{equation} y(t_{i+1})= y(t_i)+hy'(t_i)+\frac{h^2}{2}y''(\xi_i), \end{equation}\]
y ya que \(y(t)\) satisface la ecuación diferencial del problema de valor inicial \(\eqref{eq-4}\),
\[\begin{equation}\tag{5}\label{eq-5} y(t_{i+1})=y(t_i)+hf(t_i, y(t_i))+\frac{h^2}{2}y''(\xi_i). \end{equation}\]
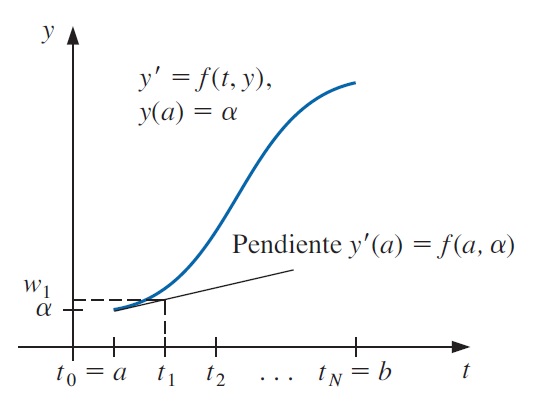
El método de Euler construye \(w_i\approx y(t_i)\), para cada \(i=1,2,..., N\), al borrar el término restante. Por lo tanto, el método de Euler es
\[\begin{equation}\tag{6}\label{eq-6} \begin{aligned} w_{0} &=\alpha, \\ w_{i+1} &=w_{i}+h f\left(t_{i}, w_{i}\right), \quad \text { para cada } i=0,1, \ldots, N-1 . \end{aligned} \end{equation}\]
Esta ecuación recibe el nombre de ecuación de diferencia relacionada con el método de Euler.
Para interpretar el método de Euler de manera geométrica, se observa que cuando \(w_i\) es una aproximación cercana para \(y(t_i)\), la suposición de que el problema está bien planteado implica que
\[\begin{equation} f(t_i, w_i)\approx y'(t_i)=f(t_i, y(t_i)) \end{equation}\]

9.2.1 Cotas del error para el método de Euler
Teorema Suponga que \(f\) es continua y satisface la condición de Lipschitz con constante \(L\) en
\[\begin{equation} D=\{(t,y)| a\leq t \leq b, -\infty <y <\infty\} \end{equation}\]
y existe una constante \(M\) con
\[\begin{equation} |y''(t)|\leq M, \qquad \forall t\in [a,b], \end{equation}\]
donde \(y(t)\) denota la única solución para el problema de valor inicial
\[\begin{equation} y'=f(t,y), \qquad a\leq t \leq b, \qquad y(a)=\alpha . \end{equation}\]
Sean \(w_0, w_1, \dots, w_N\) las aproximaciones generadas por el método de Euler para un entero positivo \(N\). Entonces, para cada \(i=0,1,2,\dots, N\),
\[\begin{equation} |y(t_i)-w_i|\leq \frac{hM}{2L}\left[e^{L(t_i-a)}-1\right]. \end{equation}\]
9.3 Métodos de Taylor de orden superior
Definición Consideremos el problema de valor inicial
\[\begin{equation} y'=f(t,y), \qquad a\leq t \leq b, \qquad y(a)=\alpha . \end{equation}\]
El método de diferencia
\[\begin{equation} \begin{aligned} w_{0} &=\alpha, \\ w_{i+1} &=w_{i}+h \phi\left(t_{i}, w_{i}\right), \quad \text { para cada } i=0,1, \ldots, N-1 . \end{aligned} \end{equation}\]
tiene error de truncamiento local
\[\begin{equation} \tau_{i+1}(h)=\frac{y_{i+1}-\left(y_{i}+h \phi\left(t_{i}, y_{i}\right)\right)}{h}=\frac{y_{i+1}-y_{i}}{h}-\phi\left(t_{i}, y_{i}\right) \end{equation}\]
para cada \(i=0, 1, \dots N-1\), donde \(y_i\) y \(y_{i+1}\) denotan la solución de la ecuación diferencial en \(t_i\) y \(t_{i+1}\), respectivamente.
Supongamos que la solución \(y(t)\) para el problema de valor inicial
\[\begin{equation} y'=f(t,y), \qquad a\leq t \leq b, \qquad y(a)=\alpha \end{equation}\]
tiene \((n+1)\) derivadas continuas. Si ampliamos la solución \(y(t)\), en términos de su enésimo polinomio de Taylor alrededor de \(t_i\) y se evalúan en \(t_{i+1}\), obtenemos
\[\begin{equation} y\left(t_{i+1}\right)=y\left(t_{i}\right)+h y^{\prime}\left(t_{i}\right)+\frac{h^{2}}{2} y^{\prime \prime}\left(t_{i}\right)+\cdots+\frac{h^{n}}{n !} y^{(n)}\left(t_{i}\right)+\frac{h^{n+1}}{(n+1) !} y^{(n+1)}\left(\xi_{i}\right), \end{equation}\]
para alguna \(\xi_i\in(t_i, t_{i+1})\).
La diferenciación sucesiva de la solución, \(y(t)\), da
\[\begin{equation} y'(t)=f(t, y(t)), \quad y''(t)=f'(t, y(t)), \text{ y en general, } y^{(k)}(t)=f^{(k-1)}(t,y(t)). \end{equation}\]
Al sustituir estos resultados en la ecuación previa, se tiene,
\[\begin{equation} \begin{aligned} y\left(t_{i+1}\right)=& y\left(t_{i}\right)+h f\left(t_{i}, y\left(t_{i}\right)\right)+\frac{h^{2}}{2} f^{\prime}\left(t_{i}, y\left(t_{i}\right)\right)+\cdots \\ &+\frac{h^{n}}{n !} f^{(n-1)}\left(t_{i}, y\left(t_{i}\right)\right)+\frac{h^{n+1}}{(n+1) !} f^{(n)}\left(\xi_{i}, y\left(\xi_{i}\right)\right) . \end{aligned} \end{equation}\]
El método de ecuación de diferencia correspondiente se obtiene al eliminar de la última ecuación el término restante relacionado con \(\xi_i\).
9.3.1 Método de Taylor de orden \(n\).
\[\begin{equation} \begin{aligned} w_{0} &=\alpha, \\ w_{i+1} &=w_{i}+h T^{(n)}\left(t_{i}, w_{i}\right), \quad \text { para cada } i=0,1, \ldots, N-1 . \end{aligned} \end{equation}\]
donde
\[\begin{equation} T^{(n)}(t_i, w_i)=f(t_i, w_i)+\frac{h}{2}f'(t_i, w_i)+\cdots+\frac{h^{n-1}}{n!}f^{(n-1)}(t_i, w_i) \end{equation}\]
El método de Euler es un método de Taylor de orden uno.
Teorema. Si se usa el método de Taylor de orden \(n\) para aproximar la solución de
\[\begin{equation} y'=f(t,y), \qquad a\leq t \leq b, \qquad y(a)=\alpha, \end{equation}\]
con tamaño de paso \(h\) y si \(y\in C^{n+1}[a,b]\), entonces el error de truncamiento local es \(O(h^n)\).
9.4 Método Runge-Kutta
Los métodos de Runge-Kutta tienen el error de truncamiento local de orden superior a los métodos de Taylor, pero eliminan la necesidad de calcular y evaluar las derivadas de \(f(t,y)\)
9.4.1 Métodos de Runge-Kutta de orden 2.
Método de punto medio
\[\begin{equation} \begin{aligned} w_{0} &=\alpha, \\ w_{i+1} &=w_{i}+h f\left(t_{i}+\frac{h}{2}, w_{i}+\frac{h}{2}f(t_i,w_i)\right), \quad \text { para cada } i=0,1, \ldots, N-1 . \end{aligned} \end{equation}\]
Método modificado de Euler
\[\begin{equation} \begin{aligned} w_{0} &=\alpha, \\ w_{i+1} &=w_{i}+\frac{h}{2} [f(t_i, w_i)+f(t_{i+1}, w_i+h\,f(t_i,w_i)], \text { para cada } i=0,1, \ldots, N-1 . \end{aligned} \end{equation}\]
9.4.2 Métodos de Runge-Kutta de orden superior
Método de Heun \(O(h^3)\)
\[\begin{equation} \begin{aligned} w_{0} &=\alpha \\ w_{i+1} &=w_{i}+\frac{h}{4}\left(f\left(t_{i}, w_{i}\right)+3\left(f\left(t_{i}+\frac{2 h}{3}, w_{i}+\frac{2 h}{3} f\left(t_{i}+\frac{h}{3}, w_{i}+\frac{h}{3} f\left(t_{i}, w_{i}\right)\right)\right)\right)\right), \end{aligned} \end{equation}\]
para \(i=0,1,\dots N-1.\)
En general, los métodos de Runge-Kutta de orden 3 no se usan. El método de Runge-Kutta que se usa de manera común es de orden 4 en forma de ecuación de diferencias, dado como sigue.
Runge-Kutta de orden 4
\[\begin{equation} \begin{array}{l} w_{0}=\alpha \\ k_{1}=h f\left(t_{i}, w_{i}\right) \\ k_{2}=h f\left(t_{i}+\frac{h}{2}, w_{i}+\frac{1}{2} k_{1}\right), \\ k_{3}=h f\left(t_{i}+\frac{h}{2}, w_{i}+\frac{1}{2} k_{2}\right), \\ k_{4}=h f\left(t_{i+1}, w_{i}+k_{3}\right), \\ w_{i+1}=w_{i}+\frac{1}{6}\left(k_{1}+2 k_{2}+2 k_{3}+k_{4}\right), \end{array} \end{equation}\]
para cada \(i=0,1,\dots, N-1\). Este método tiene error de truncamiento local \(O(h^4)\), siempre y cuando la solución \(y(t)\) tenga cinco derivadas continuas.