6 Interpolación
Consultar el Capítulo 17: Interpolation.
6.1 Polinomios de interpolación de Lagrange
El problema de determinar un polinomio de grado uno que pasa por diferentes puntos \((x_0, y_0)\) y \((x_1, y_1)\) es equivalente al de aproximar la función \(f\) para la que \(f(x_0)=y_0\) y \(f(x_1)=y_1\) por medio de un polinomio de primer grado que se interpola, o que coincida con los valores de \(f\) en los puntos determinados. El uso de estos polinomios para aproximación dentro del intervalo determinado mediante puntos finales recibe el nombre de interpolación.
Definimos las funciones
\[\begin{equation} L_0(x)=\frac{x-x_1}{x_0-x_1}\qquad y \qquad L_1(x)=\frac{x-x_0}{x_1-x_0}. \end{equation}\]
El polinomio de interpolación de Lagrange lineal a través de \((x_0, y_0)\) y \((x_1, y_1)\) es
\[\begin{equation} P(x)=L_0(x)f(x_0)+L_1(x)f(x_1)=\frac{x-x_1}{x_0-x_1}f(x_0)+\frac{x-x_0}{x_1-x_0}f(x_1). \end{equation}\]
Obsérvese que
\[\begin{equation} L_0(x_0)=1, \qquad L_0(x_1)=0, \qquad L_1(x_0)=0, \qquad L_1(x_1)=1, \end{equation}\]
lo cual implica que
\[\begin{equation} P(x_0)=1\cdot f(x_0)+0\cdot f(x_1)=f(x_0)=y_0 \end{equation}\]
y
\[\begin{equation} P(x_1)=0\cdot f(x_0)+1\cdot f(x_1)=f(x_1)=y_1 \end{equation}\]
por lo que \(P\) es el único polinomio de grado a lo más 1 que pasa por \((x_0, y_0)\) y \((x_1, y_1)\).
Para generalizar el concepto de interpolación lineal, consideramos la construcción de un polinomio de grado \(n\) que pasa a través de \(n+1\) puntos
\[\begin{equation} (x_0, f(x_0)), \quad (x_1, f(x_1)), \quad \dots \quad, (x_n, f(x_n)). \end{equation}\]
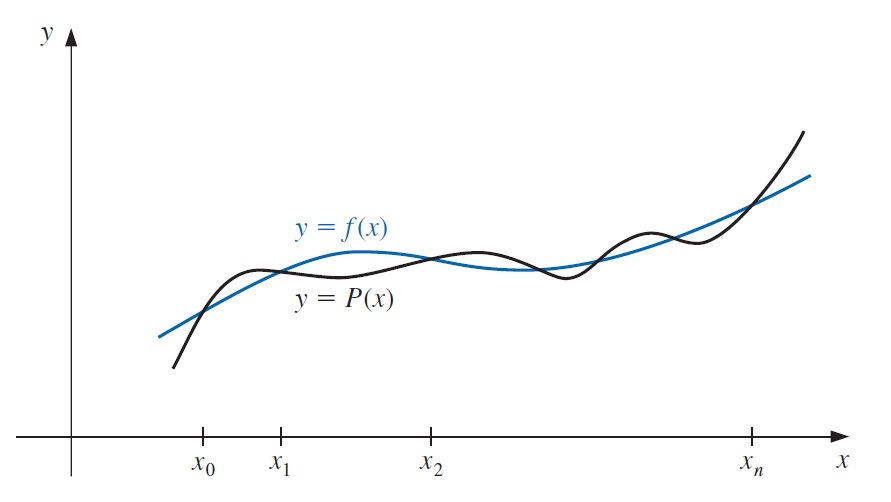
En este caso, primero construimos para cada \(k=0,1,\dots, n\) una función \(L_{n,k}(x)\) con la propiedad de que \(L_{n,k}(x_i)=0\) cuando \(i\neq k\) y \(L_{n,k}(x_k)=1\). Para satisfacer \(L_{n,k}(x_i)=0\) para cada \(i\neq k\) se requiere que el numerador de \(L_{n,k}(x)\) contenga los factores
\[\begin{equation} (x-x_0)(x-x_1)\cdots (x-x_{k-1})(x-x_{k+1})\cdots (x-x_n). \end{equation}\]
Para satisfacer \(L_{n,k}(x_k)=1\), el denominador de \(L_{n,k}(x)\) debe ser el mismo término, pero evaluado en \(x=x_k\). Por lo tanto
\[\begin{equation} L_{n, k}(x)=\frac{\left(x-x_{0}\right) \cdots\left(x-x_{k-1}\right)\left(x-x_{k+1}\right) \cdots\left(x-x_{n}\right)}{\left(x_{k}-x_{0}\right) \cdots\left(x_{k}-x_{k-1}\right)\left(x_{k}-x_{k+1}\right) \cdots\left(x_{k}-x_{n}\right)} . \end{equation}\]
Un bosquejo de la gráfica de una \(L_{n,k}\) (cuando \(n\) es par) se muestra a continuación.

El polinomio de interplación se describe fácilmente una vez que se conoce la forma \(L_{n,k}\). Este polinomio, llamado enésimo polinomio de interpolación de Lagrange, se define en el siguiente teorema.
Teorema 6.1 Si \(x_0, x_1, ..., x_n\) son \(n+1\) números distintos y \(f\) es una función cuyos valores están determinados en estos números, entonces existe un único polinomio \(P(x)\) de grado a lo sumo \(n\) con
\[\begin{equation} f(x_k)=P(x_k), \text{ para cada } k=0,1,\dots, n. \end{equation}\]
Este polinomio está determinado por
\[\begin{equation} P(x)=f(x_0)L_{n,0}(x)+\cdots + f(x_n)L_{n,n}(x)=\sum_{k=0}^n f(x_k)L_{n,k}(x), \end{equation}\]
donde, para cada \(k=0,1, \dots, n\),
\[\begin{equation} \begin{aligned} L_{n, k}(x) &=\frac{\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{k-1}\right)\left(x-x_{k+1}\right) \cdots\left(x-x_{n}\right)}{\left(x_{k}-x_{0}\right)\left(x_{k}-x_{1}\right) \cdots\left(x_{k}-x_{k-1}\right)\left(x_{k}-x_{k+1}\right) \cdots\left(x_{k}-x_{n}\right)} \\ &=\prod_{i=0 \atop i \neq k}^{n} \frac{\left(x-x_{i}\right)}{\left(x_{k}-x_{i}\right)} . \end{aligned} \end{equation}\]
Escribirimos \(L_{n,k}(x)\) simplemente como \(L_k(x)\) cuando no haya confusión en cuanto a su grado.
Teorema 6.2 Suponga que \(x_0, x_1, ..., x_n\) son números distintos en el intervalo \([a,b]\) y \(f\in C^{n+1}[a,b]\). Entonces, para cada \(x\in [a,b]\), existe un número \(\xi (x)\) (generalmente no conocido) entre \(mín\{x_0, x_1, \dots, x_n\}\) y \(max\{x_0, x_1, \dots, x_n\}\) y, por lo tanto, en \((a,b)\), con
\[\begin{equation} f(x)=P(x)+\frac{f^{(n+1)}(\xi (x))}{(n+1)!}(x-x_0)(x-x_1)\cdots (x-x_n), \end{equation}\]
donde \(P(x)\) es el polinomio de interpolación determinado en el teorema anterior.
La forma del error para el polinomio de Lagrange es bastante similar a la del polinomio de Taylor. El enésimo polinomio de Taylor alrededor de \(x_0\) concentra toda la información conocida en \(x_0\) y tiene un término de error de la forma
\[\begin{equation} \frac{f^{(n+1)}(\xi (x))}{(n+1)!}(x-x_0)^{n+1} \end{equation}\]
El polinomio de Lagrange de grado \(n\) utiliza información en los distintos números \(x_0, x_1, \dots, x_n\) y, en lugar de \((x-x_0)^{n+1}\) su fórmula de error utiliza el producto de los \(n+1\) términos \((x-x_0), (x-x_1)\cdots (x-x_n)\)
\[\begin{equation} \frac{f^{(n+1)}(\xi (x))}{(n+1)!}(x-x_0)(x-x_1)\cdots (x-x_n). \end{equation}\]
6.2 Diferencias divididas (Newton)
Supongamos que \(P_n(x)\) es el enésimo polinomio de interpolación que concuerda con la función \(f\) en los diferentes números \(x_0, x_1, \dots, x_n\). A pesar que este polinomio es único, existen representaciones algebraicas que son útiles en ciertas situaciones. Las diferencias divididas de \(f\) respecto a \(x_0, x_1, \dots, x_n\) se usan para expresar \(P_n(x)\) en la forma
\[\begin{equation} P_n(x) = a_0 + a_1(x-x_0) + a_2 (x-x_0)(x-x_1)+\cdots + a_n (x-x_0)\cdots (x-x_{n-1}) \end{equation}\]
para constantes apropiadas \(a_0, a_1, \dots, a_n\). Para determinar la primera de estas constantes, \(a_0\), observemos que si \(P_n(x)\) se escribe como en la ecuación anterior, entonces evaluando \(P_n(x)\) en \(x_0\) queda sólo el término constante \(a_0\); es decir,
\[\begin{equation} a_0=P_n(x_0)=f(x_0) \end{equation}\]
De manera análoga, cuando \(P(x)\) se evalúa en \(x_1\), los únicos términos diferentes de cero en la evaluación de \(P_n(x_1)\) son los términos constante y lineal,
\[\begin{equation} f(x_0)+a_1(x_1-x_0)=P_n(x_1)=f(x_1) \end{equation}\]
por lo que
\[\begin{equation}\tag{6.1}\label{eq-6.1} a_1 = \frac{f(x_1)-f(x_0)}{x_1-x_0}. \end{equation}\]
Ahora se presentará la notación de diferencias divididas, la ceroésima diferencia dividida de \(f\) respecto a \(x_i\), denotada \(f[x_i]\), es simplemente el valor de \(f\) en \(x_i\),
\[\begin{equation} f[x_i]=f(x_i). \end{equation}\]
Las diferencias divididas restantes se definen de manera recursiva; la primera diferencia divididida de \(f\) respecto a \(x_i\) y \(x_{i+1}\) se denota \(f[x_i, x_{i+1}]\) y se define como
\[\begin{equation} f[x_i, x_{i+1}] = \frac{f[x_{i+1}]-f[x_i]}{x_{i+1}-x_i} \end{equation}\]
La segunda diferencia dividida \(f[x_i, x_{i+1}, x_{i+2}]\) se define como
\[\begin{equation} f[x_i, x_{i+1}, x_{i+2}] = \frac{f[x_{i+1}, x_{i+2}]-f[x_i, x_{i+1}]}{x_{i+2}-x_i} \end{equation}\]
De igual forma, después de que las \((k-1)\)-ésimas diferencias divididas,
\[\begin{equation} f[x_i, x_{i+1}, x_{i+2}, \dots, x_{i+k-1}] \quad \text{ y } \quad f[x_{i+1}, x_{i+2}, \dots, x_{i+k-1}, x_{i+k}], \end{equation}\]
se han determinado, la \(k\)-ésima diferencia dividida relativa a \(x_i, x_{i+1}, x_{i+2}, \dots x_{i+k}\) es
\[\begin{equation} f[x_i, x_{i+1}, \dots, x_{i+k-1}, x_{i+k}] = \frac{f[x_{i+1}, x_{i+2}, \dots, x_{i+k}]- f[x_{i}, x_{i+1}, \dots, x_{i+k-1}]}{x_{i+k}-x_i}. \end{equation}\]
El proceso termina con la única enésima diferencia dividida,
\[\begin{equation} f[x_0, x_{1}, \dots, x_{n}] = \frac{f[x_{1}, x_{2}, \dots, x_{n}]- f[x_{0}, x_{1}, \dots, x_{n-1}]}{x_{n}-x_0}. \end{equation}\]
Debido a la ecuación \(\eqref{eq-6.1}\) podemos escribir \(a_1= f[x_0, x_1]\), justo cuando \(a_0\) se puede expresar como \(a_0=f(x_0)=f[x_0]\). Por lo tanto, el polinomio de interpolación es
\[\begin{equation} P_n(x)= f[x_0] + f[x_0, x_1] (x-x_0) + a_2 (x-x_0)(x-x_1)+\cdots + a_n (x-x_0)\cdots (x-x_{n-1}) \end{equation}\]
Como se puede esperar a partir de la evaluación de \(a_0\) y \(a_1\), las constantes requeridas son
\[\begin{equation} a_k = f[x_0, x_1, x_2, \dots, x_k], \end{equation}\]
para cada \(k=0, 1, \dots, n\). Por lo que el polinomio se puede reescribir en una forma llamada diferencias divididas de Newton:
\[\begin{equation} P_n(x) = f[x_0] + \sum_{k=1}^n f[x_0, x_1, \dots,x_k] (x-x_0)\cdots (x-x_{k-1}) \end{equation}\]
El valor de \(f[x_0, x_1, \dots, x_k]\) es independiente del orden de los números \(x_0, x_1,\dots, x_k\). La generación de las diferencias divididas se describe en la siguiente tabla, a partir de estos datos también se pueden determinar dos cuartas y una quinta diferencia.

6.3 Interpolación de spline cúbico
En esta sección se aborda la aproximación polinomial por tramos.
6.3.1 Aproximación de polinomios por tramos
La aproximación polinomial por tramos más simple es la interpolación lineal por tramos, la cual consiste en unir un conjunto de puntos de datos
\[\begin{equation} \{ (x_0, f(x_0)), (x_1, f(x_1)),\dots, (x_n, f(x_n)) \} \end{equation}\]
mediante una serie líneas rectas.
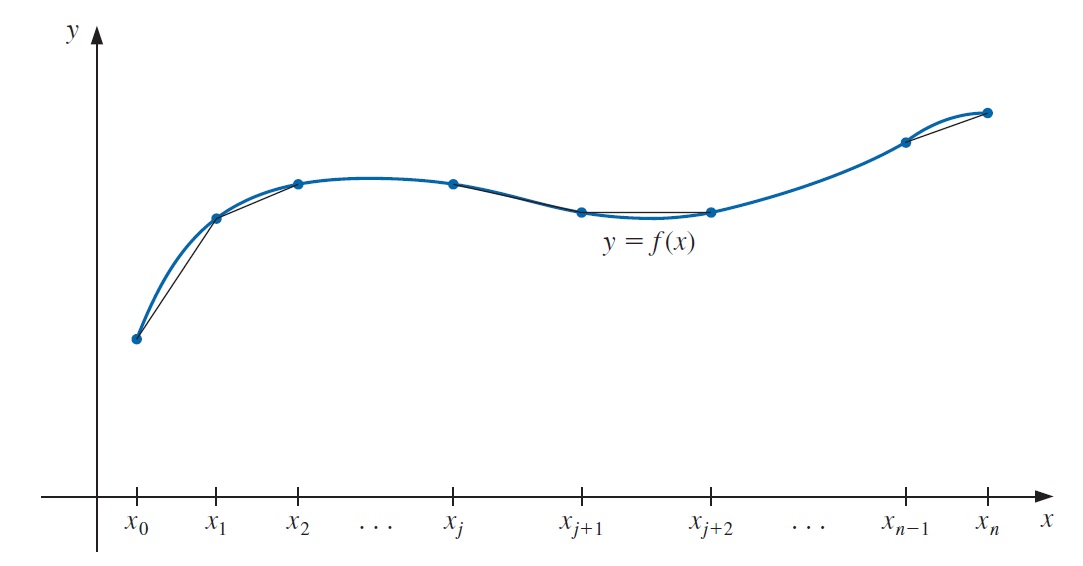
6.3.2 Splines cúbicos
La aproximación polinomial por tramos más común usa polinomios cúbicos entre cada par sucesivo de nodos y recibe el nombre de interpolación de spline cúbico.

Definición 6.1 Dada una función \(f\) definida en \([a,b]\) y un conjunto de nodos \(a=x_0<x_1<\cdots <x_n=b\), una interpolación por splines cúbicos \(S\) para \(f\) es una función que satisface las siguientes condiciones:
\(S(x)\) es un polinomio cúbico, que se denota \(S_j(x)\), en el intervalo \([x_j, x_{j+1}]\) para cada \(j=0,1,\dots, n-1\);
\(S_j(x_j)=f(x_j)\) y \(S_j(x_{j+1})=f(x_{j+1})\) para cada \(j=0,1,\dots, n-1\);
\(S_{j+1}(x_{j+1})=S_j(x_{j+1})\) para cada \(j=0,1,\dots, n-2\); (implícito en \(b\))
\(S'_{j+1}(x_{j+1})=S'_j(x_{j+1})\) para cada \(j=0,1,\dots, n-2\);
\(S''_{j+1}(x_{j+1})=S''_j(x_{j+1})\) para cada \(j=0,1,\dots, n-2\);
Uno de los siguientes conjuntos de condiciones de frontera se satisface:
\(S''(x_0)=S''(x_n)=0\), (frontera natural o libre);
\(S'(x_0)=f'(x_0)\) y \(S'(x_n)=f'(x_n)\) (frontera condicionada).
6.3.3 Construcción de un spline cúbico
Un spline definido en un intervalo que se ha dividido en \(n\) subintervalos requerirá determinar \(4n\) constantes. Para construir el spline cúbico que se interpola para una función dada \(f\), las condiciones en la definición se aplican a los polinomios cúbicos
\[\begin{equation} S_j(x)=a_j+b_j(x-x_j)+c_j(x-x_j)^2+d_j(x-x_j)^3 \end{equation}\]
para cada \(j=0,1,\dots, n-1\). Puesto \(S_j(x_j)=a_j=f(x_j)\), la condición \(c)\) se puede aplicar para obtener
\[\begin{equation} a_{j+1}=S_{j+1}\left(x_{j+1}\right)=S_{j}\left(x_{j+1}\right)=a_{j}+b_{j}\left(x_{j+1}-x_{j}\right)+c_{j}\left(x_{j+1}-x_{j}\right)^{2}+d_{j}\left(x_{j+1}-x_{j}\right)^{3} \end{equation}\]
para cada \(j=0,1,\dots, n-2\).
Como los términos \(x_{j+1}-x_j\) son usados repetidamente en este desarrollo, es conveniente introducir una notación más simple
\[\begin{equation} h_j=x_{j+1}-x_j, \end{equation}\]
para cada \(j=0,1,\dots, n-1\). Si también definimos \(a_n=f(x_n)\), entonces la ecuación
\[\begin{equation} a_{j+1} =a_j+b_jh_j+c_jh^2_j+d_jh^3_j \end{equation}\]
se mantiene para cada \(j=0,1,\dots, n-1\).
De manera similar, defina \(b_n=S'(x_n)\) y observe que
\[\begin{equation} S'_j(x)=b_j+2c_j(x-x_j)+3d_j(x-x_j)^2 \end{equation}\]
implica que \(S'_j(x_j)=b_j\), para cada \(j=0,1,\dots, n-1\). Al aplicar la condición en la parte \(d)\) obtenemos
\[\begin{equation} b_{j+1}=b_j+2c_jh_j+3d_jh^2_j, \end{equation}\]
para cada \(j=0,1,\dots, n-1\).
Otra relación entre los coeficientes de \(S_j\) se obtiene al definir \(c_n=S''(x_n)/2\) y aplicar la condición en la parte \(e)\). Entonces para cada \(j=0,1,\dots, n-1\),
\[\begin{equation} c_{j+1}=c_j+3d_jh_j. \end{equation}\]
Resolviendo para \(d_j\) y sustituyendo este valor en las ecuaciones anteriores obtenemos para cada \(j=0,1,\dots, n-1\), las nuevas ecuaciones
\[\begin{equation} a_{j+1}=a_j+b_jh_j+\frac{h^2_j}{3}(2c_j+c_{j+1}) \end{equation}\]
y
\[\begin{equation} b_{j+1}=b_j+h_j(c_j+c_{j+1}). \end{equation}\]
La relación final que incolucra los coeficientes se obtiene al resolver la penúltima ecuación, primero para \(b_j\)
\[\begin{equation} b_j=\frac{1}{h_j}(a_{j+1}-a_j)-\frac{h_j}{3}(2c_j+c_{j+1}), \end{equation}\]
y entonces, con una reducción del índice, para \(b_{j-1}\). Esto nos da
\[\begin{equation} b_{j-1}=\frac{1}{h_{j-1}}(a_j+-a_{j-1})-\frac{h_j}{3}(2c_{j-1}+c_{j}). \end{equation}\]
Al sustituir estos valores en la ecuación obtenida, con el índice reducido en uno, obtenemos el sistema lineal de ecuaciones
\[\begin{equation} h_{j-1} c_{j-1}+2\left(h_{j-1}+h_{j}\right) c_{j}+h_{j} c_{j+1}=\frac{3}{h_{j}}\left(a_{j+1}-a_{j}\right)-\frac{3}{h_{j-1}}\left(a_{j}-a_{j-1}\right) \end{equation}\]
Para cada \(j=1,2,..., n-1\). Este sistema sólo tiene los \(\{c_j\}_{j=0}^n\) como incógnitas. Los valores \(\{h_j\}_{j=0}^n\) y \(\{a_j\}_{j=0}^n\) están dados, respectivamente, por el espaciado de los nodos \(\{x_j\}_{j=0}^n\) y los valores de \(f\) en los nodos. Por lo que, una vez que se determinal los valores de \(\{c_j\}_{j=0}^n\), se pueden determinar el resto de las constantes \(\{b_j\}_{j=0}^{n-1}\) y \(\{d_j\}_{j=0}^{n-1}\). Entonces podemos construir los polinomios cúbicos \(\{S_j(x)\}_{j=0}^{n-1}\).
Teorema 6.3 Si \(f\) se define en \(a=x_0<x_1<\cdots <x_n=b\), entonces \(f\) tiene un spline natural único que interpola \(S\) en los nodos \(x_0, x_1, \dots, x_n\); es decir, un spline interpolante que satisface las condiciones de frontera natural \(S''(a)=0\) y \(S''(b)=0\).