6 Técnicas de conteo
6.1 Principio de multiplicación
Proposición 6.1 Si un procedimiento \(A_1\) puede efectuarse de \(m\) formas distintas y un segundo procedimiento \(A_2\) puede realizarse de \(n\) formas diferentes, entonces el total de formas en que puede efectuarse el primer procedimiento, seguido del segundo es el producto \(mn\), es decir
\[\begin{equation*} \#(A_1\times A_2)=\#A_1\cdot \#A_2. \end{equation*}\]
El principio de multiplicación es válido para cualquier sucesión finita de procedimientos, donde, \(A_1,A_2,...,A_k\) denotan \(k\) procedimientos sucesivos, donde el procedimiento \(A_i\) se puede efectuar de \(n_i\) formas distintas, \(i=1,...,k\). Entonces, hay un total de \(n_1n_2\cdots n_k\) formas de realizar los \(k\) procedimientos de manera sucesiva.
Ejemplo 6.1 ¿Cuántas secuencias son posibles cuando se tira un dado cuatro veces?
Ejemplo 6.2 En una cadena proteica de 100 aminoácidos de longitud, en cada posición puede haber cualquiera de los 20 aminoácidos ¿Cuál es el número de proteínas distintas, con secuencia única que se pueden formar?
Ejemplo 6.3 20 trabajadores son asignados a 20 diferentes trabajos, uno a cada trabajo. ¿Cuántas asignaciones diferentes son posibles?
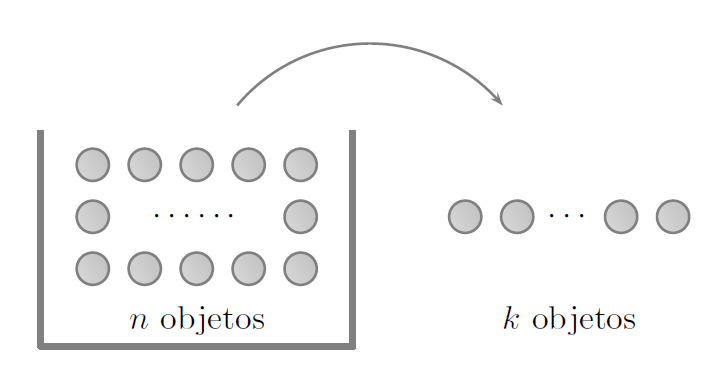
A continuación se considerarán diferentes esquemas y contextos donde es posible encontrar una fórmula matemática para ciertos problemas de conteo. El esquema general es el de extraer al azar \(k\) objetos de una urna con \(n\) objetos distintos.
A la colección de objetos seleccionados le llamaremos muestra.
6.2 Ordenaciones con repetición: muestras con orden y con reemplazo
Supongamos que de la urna con \(n\) objetos distintos se requiere realizar \(k\) extracciones al azar de un objeto a la vez. Al efectuar una extracción, se registra el objeto y se regresa a la urna, de esta manera el mismo objeto puede ser extraído varias veces.
El total de arreglos que se pueden obtener de esta urna al hacer \(k\) extracciones de estas características es el número \(n^k\), el cual es llamado ordenaciones con repetición y es denotado por
\[\begin{equation*} OR_n^k=n^k \end{equation*}\]
Ejemplo 6.4 Suponga que tenemos un conjunto de 60 caracteres diferentes. Este conjunto contiene algunas letras minúsculas del alfabeto, sus correspondientes letras mayúsculas y los diez dígitos numéricos ¿Cuántos passwords de longitud 4 se pueden construir usando este conjunto de 60 caracteres?
6.3 Ordenaciones sin repetición: muestras con orden y sin reemplazo
La situación en este caso es: de la urna con \(n\) objetos se deben extraer, uno a uno, \(k\) objetos. Supóngase esta vez que la selección es sin reemplazo, es decir, una vez seleccionado un objeto, éste ya no se reincorpora a la urna. El total de arreglos distintos que se pueden obtener de este modo es el número
\[\begin{equation*} n(n-1)(n-2)\cdots (n-k+1) \end{equation*}\]
el cual es llamado ordenaciones (o permutaciones) de \(n\) en \(k\) y puede escribirse como sigue
\[\begin{equation*} O_n^k=\frac{n!}{(n-k)!} \end{equation*}\]
En el caso particular cuando la selección es exhaustiva, es decir, cuando \(k=n\), se tienen todas las permutaciones o distintos órdenes en que se pueden colocar \(n\) objetos, es decir \(n!\).
6.4 Permutaciones: muestras exhausivas con orden y sin reemplazo
Definición 6.1 Dada una colección de \(n\) objetos distintos, cualquier disposición (lineal) u ordenamiento de estos objetos se denomina permutación de la colección.
Proposición 6.2 Dada una colección de \(n\) objetos distintos existen
\[\begin{equation*} n(n-1)(n-2)\cdots 3\cdot 2 \cdot 1=n! \end{equation*}\]
permutaciones diferentes.
Por conveniencia se define \(0!=1\).
Ejemplo 6.5 Si se desea conocer el total de formas distintas en que se puede desordenar una enciclopedia de 5 volúmenes en un librero, la respuesta es \(5!=120\).
6.5 Combinaciones: muestras sin orden y sin reemplazo
Supongamos que se tiene un conjunto de \(n\) objetos distinguibles y nos interesa obtener una muestra de tamaño \(k\), pero en este caso las muestras deben ser sin orden y sin reemplazo, es decir, la muestra se considera como un conjunto pues no hay repeticiones ni orden entre sus elementos.
Proposición 6.3 El número de grupos diferentes de tamaño \(k\) que pueden ser seleccionados de un conjunto de \(n\) objetos cuando el orden de selección no es relevante es dado por
\[\begin{equation*} \left( \begin{array}{c} n\\ k \end{array} \right)=\frac{n!}{(n-k)! k!} \quad k\leq n, \end{equation*}\]
el cual es llamado coeficiente binomial y también es denotado por \(C_n^k\).
Ejemplo 6.6 7 diferentes regalos deber ser distribuidos entre 10 niños. ¿Cuántos resultados son posibles si ningún niño recibe más de un regalo?
Teorema 6.1 Para cualesquiera números reales \(x,y\), y para cualquier número entero \(n\geq 0\), \[\begin{equation*} (x+y)^n=\sum_{k=0}^n \left( \begin{array}{c} n\\ k \end{array} \right) x^{n-k} y^{k} \end{equation*}\]
6.6 Coeficiente multinomial
Considérense \(n\) objetos no necesariamente distintos unos de otros, supongamos que se tienen \(k_1\) objetos de un primer tipo, \(k_2\) objetos de un segundo tipo, y así sucesivamente, hasta \(k_m\) objetos del tipo \(m\), en donde \(k_1+k_2+\cdots+k_m=n\). Estos \(n\) objetos pueden ordenarse uno detrás de otro de tantas maneras como lo indica el coeficiente multinomial
\[\begin{equation*} \binom{n}{k_1k_2\cdots k_m}=\frac{n!}{k_1!k_2!\cdots k_m!}. \end{equation*}\]
El teorema binomial puede extenderse al denominado teorema del multinomio que establece
\[\begin{equation*} (a_1+a_2+\cdots+a_m)^n=\sum \binom{n}{k_1k_2\cdots k_m} a_1^{k_1}a_2^{k_2}\cdots a_m^{k_m} \end{equation*}\]
donde la suma se efectúa sobre todos los posibles valores enteros no negativos de \(k_1, k_2,..., k_m\) tales que \(k_1+k_2+...+ k_m=n\).
6.7 Muestras sin orden y con reemplazo
Consideremos el caso de hacer \(k\) extracciones de una urna de \(n\) objetos con las condiciones de que cada objeto extraído es regresado a la urna (y puede ser elegido nuevamente), y en donde el orden de la muestra no es relevante.
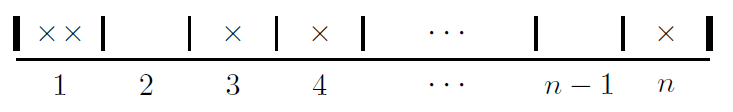
El número total de arreglos es
\[\begin{equation*} \binom{n+k-1}{k} \end{equation*}\]
que equivale a colocar dentro de las \(n+k-1\) posiciones las \(k\) cruces, dejando en los lugares restantes las paredes movibles.
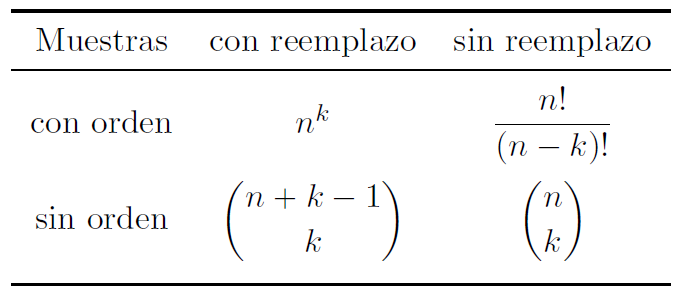
Resumen de fórmulas.
Ejemplo 6.7 Si 4 españoles, 3 franceses y 3 británicos se sientan en línea. ¿Cuántos posibles arreglos hay cuando las personas de la misma nacionalidad deben sentarse una al lado de otra?
Ejemplo 6.8 Una niña tiene 12 bloques, de los cuales 6 son negros, 4 rojos, 1 blanco y uno es azul. Si la niña coloca los bloques en línea ¿cuántos arreglos son posibles?
Ejemplo 6.9 Si 12 personas son divididas en 3 comités de respectivos tamaños 3, 4 y 5. ¿Cuántas divisiones son posibles?
Ejemplo 6.10 Considere la siguiente cuadrícula. Supóngase que, comenzando en el punto \(A\), se puede dar un paso hacia arriba o uno a la derecha en cada movimiento. Este procedimiento concluye hasta llegar al punto \(B\). ¿Cuántas rutas diferentes de \(A\) a \(B\) son posibles?

Ejemplo 6.11 Sean \(A\) y \(B\) dos conjuntos finitos con cardinalidades \(n\) y \(m\), respectivamente. Determine el número total de funciones \(f:A\rightarrow B\) tal que
no tienen restricción alguna.
son inyectivas, suponiendo que \(n\leq m\).
son sobreyectivas, suponiendo que \(m\leq n\).